山东省济南市天桥区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 下列各数中是无理数的是( )A、-3 B、π C、9 D、-0.112. 在平面直角坐标系中,点(1,-3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列命题中,是真命题的是( )A、内错角相等 B、三角形的外角大于内角 C、对顶角相等 D、同位角互补,两直线平行4. 计算×的结果是( )A、 B、4 C、 D、25. 关于正比例函数y=-3x,下列结论正确是( )A、图象不经过原点 B、y的值随着x增大而增大 C、图象经过二、四象限 D、当x=1时,y=36. 如图,已知CD∥BE,如果∠1=60°,那么∠B的度数为( )
 A、70° B、100° C、110° D、120°7. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
A、70° B、100° C、110° D、120°7. 在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:成绩(m)
1.50
1.60
1.65
1.70
1.75
1.80
人数(人)
1
2
4
3
3
2
这些运动员跳高成绩的中位数和众数分别是( )
A、1.70m,1.65m B、1.70m,1.70m C、1.65m,1.65m D、3人,4人8. 已知正比例函数y=kx的函数值y随x的增大而增大,则一次函数y=x﹣k的图象是( )A、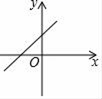 B、
B、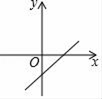 C、
C、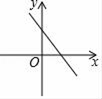 D、
D、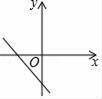 9. 篮球比赛中,每场比赛都要分出胜负,每队胜1场得3分,负一场扣1分。某队在8场比赛中得到12分,若设该该队胜的场数为x,负的场数为y,则可列方程组为( )A、 B、 C、 D、10. 如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F .若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )
9. 篮球比赛中,每场比赛都要分出胜负,每队胜1场得3分,负一场扣1分。某队在8场比赛中得到12分,若设该该队胜的场数为x,负的场数为y,则可列方程组为( )A、 B、 C、 D、10. 如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F .若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( ) A、35° B、40° C、45° D、50°11. 如图,△ABC、△CDE都是等腰三角形,且CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点O,点M,N分别是线段AD,BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC,则OC平分∠AOE.正确是( )
A、35° B、40° C、45° D、50°11. 如图,△ABC、△CDE都是等腰三角形,且CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点O,点M,N分别是线段AD,BE的中点,以下4个结论:①AD=BE;②∠DOB=180°-α;③△CMN是等边三角形;④连OC,则OC平分∠AOE.正确是( ) A、①②③ B、①②④ C、①③④ D、①②③④12. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )
A、①②③ B、①②④ C、①③④ D、①②③④12. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图象能大致反映y与x函数关系的是( )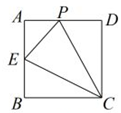 A、
A、 B、
B、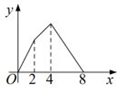 C、
C、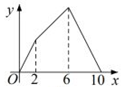 D、
D、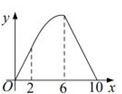
二、填空题
-
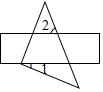
13. 点P(-2, 3)关于x轴对称的点的坐标为14. 把一块含有 角的直角三角板与两条长边平行的直尺如图放置(直角顶点在直尺的一条长边上).若 ,则 .
 15. 现有甲乙两个合唱队,他们的平均身高都是170cm,方差分别是S2甲、S2乙 , 且S2甲>S2乙 , 则两个队队员的身高较整齐的是队(填甲或乙)。
15. 现有甲乙两个合唱队,他们的平均身高都是170cm,方差分别是S2甲、S2乙 , 且S2甲>S2乙 , 则两个队队员的身高较整齐的是队(填甲或乙)。
16. 已知三角形三边长分别是6,8,10,则此三角形的面积为 .17. 在四边形ABCD中,∠A=∠ABC=90°,△BCD为等边三角形,且AD=2,则四边形ABCD的周长为 18. 在平面直角坐标系中,若干个边长为 个单位长度的等边三角形,按如图中的规律摆放.点 从原点 出发,以每秒 个单位长度的速度沿着等边三角形的边“ …”的路线运动,设第 秒运动到 点为正整数),则点 的坐标是 .
18. 在平面直角坐标系中,若干个边长为 个单位长度的等边三角形,按如图中的规律摆放.点 从原点 出发,以每秒 个单位长度的速度沿着等边三角形的边“ …”的路线运动,设第 秒运动到 点为正整数),则点 的坐标是 .
三、解答题
-
19. 计算: -320. 解方程组:21. 如图所示,已知AD∥BC,BE平分∠ABC,∠A=110°.求∠ADB的度数.
 22. 如图,已知点 为 的边 的中点, ,垂足分别为 ,且 .
22. 如图,已知点 为 的边 的中点, ,垂足分别为 ,且 .
求证:
(1)、(2)、 平分23. 体育器材室有A、B两种型号的实心球,1只A型球与1只B型球的质量共7千克,3只A型球与1只B型球的质量共13千克.(1)、每只A型球、B型球的质量分别是多少千克?(2)、现有A型球、B型球的质量共17千克,则A型球、B型球各有多少只?24. 为宣传6月6日世界海洋日,某校八年级举行了主题为“珍海洋资源,保护海洋生物多科性“的知识党春活动,为了解此次宛赛成镇(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图):
请根据图表信息解答以下问题:
(1)、本次调查一共随机抽取了个参赛学生的成绩;(2)、a= , b=.(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是(4)、请你估计,该校八年级全年级有500名学生,竞赛成绩达到80分以上(含80分)的学生约有多少人?25. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题: (1)、小帅的骑车速度为千米/小时;点C的坐标为;(2)、求线段AB对应的函数表达式;(3)、当小帅到达乙地时,小泽距乙地还有多远?26. 如图1,在平面直角坐标系中,OA=OB,点B的坐标为(1,0),AB= ,线段OB上的动点(点C不与O、B重合),连接AC,作AC⊥CD,作DE⊥x轴,垂足为点E.
(1)、小帅的骑车速度为千米/小时;点C的坐标为;(2)、求线段AB对应的函数表达式;(3)、当小帅到达乙地时,小泽距乙地还有多远?26. 如图1,在平面直角坐标系中,OA=OB,点B的坐标为(1,0),AB= ,线段OB上的动点(点C不与O、B重合),连接AC,作AC⊥CD,作DE⊥x轴,垂足为点E. (1)、求证:△ACO≌△CDE;(2)、猜想△BDE的形状,并证明结论:(3)、如图2,当△BCD为等腰三角形时,求点D的坐标.27. 如图,在△ABC中,∠ACB=90°,AC=BC, E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE, CG平分∠ACB交BD于点G,
(1)、求证:△ACO≌△CDE;(2)、猜想△BDE的形状,并证明结论:(3)、如图2,当△BCD为等腰三角形时,求点D的坐标.27. 如图,在△ABC中,∠ACB=90°,AC=BC, E为AC边的一点,F为AB边上一点,连接CF,交BE于点D,且∠ACF=∠CBE, CG平分∠ACB交BD于点G, (1)、如图1,求证:CF=BG;(2)、如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,
(1)、如图1,求证:CF=BG;(2)、如图2,延长CG交AB于H,连接AG,过点C作CP∥AG交BE的延长线于点P,求证:PB=CP+CF;
(3)、如图3,在(2)间的条件下,当∠GAC=2∠FCH时,若S△AEG=3 ,BG=6,求AC的长.