山东省德州市德城区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-17 类型:期末考试
一、单选题
-
1. 低碳环保理念深入人心,共享单车已成为出行新方式.下列共享单车图标,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一次抽奖活动特等奖的中奖率为 ,把 用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 在 , , , , ,中分式的个数有( )A、2个 B、3个 C、4个 D、5个5. 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
2. 一次抽奖活动特等奖的中奖率为 ,把 用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 在 , , , , ,中分式的个数有( )A、2个 B、3个 C、4个 D、5个5. 在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形(如图),通过计算图形(阴影部分)的面积,验证了一个等式,则这个等式是( ) A、a2-b2=(a+b)(a-b) B、(a+b)2=a2+2ab+b2 C、(a-b)2=a2-2ab+b2 D、a2-ab=a(a-b)6. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径面弧,两弧交于点 ,作射线 交边 于点 ,若 ,则 的面积是( )
A、a2-b2=(a+b)(a-b) B、(a+b)2=a2+2ab+b2 C、(a-b)2=a2-2ab+b2 D、a2-ab=a(a-b)6. 如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 于点 ,再分别以点 为圆心,大于 的长为半径面弧,两弧交于点 ,作射线 交边 于点 ,若 ,则 的面积是( )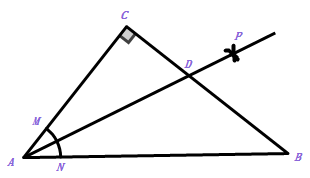 A、 B、 C、 D、7.
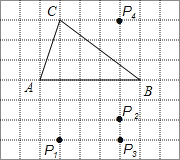
A、 B、 C、 D、7.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
 A、1个 B、2个 C、3个 D、4个8. 下列说法不正确的是( ).A、关于某条直线对称的两个三角形一定全等. B、到线段两端点距离相等的点有无数个. C、等腰三角形的中线、高、角平分线三线合一. D、轴对称图形的对称轴是对称点所连线段的垂直平分线.9. 已知a,b,c是三角形的三边,那么代数式a2-2ab+b2-c2的值( )A、大于零 B、等于零 C、小于零 D、不能确定10. 小明坐滴滴打车前去火车高铁站,小明可以选择两条不同路线:路线A的全程是25千米,但交通比较拥堵,路线B的全程比路线A的全程多7千米,但平均车速比走路线A时能提高60%,若走路线B的全程能比走路线A少用15分钟.若设走路线A时的平均速度为x千米/小时,根据题意,可列分式方程( )
A、1个 B、2个 C、3个 D、4个8. 下列说法不正确的是( ).A、关于某条直线对称的两个三角形一定全等. B、到线段两端点距离相等的点有无数个. C、等腰三角形的中线、高、角平分线三线合一. D、轴对称图形的对称轴是对称点所连线段的垂直平分线.9. 已知a,b,c是三角形的三边,那么代数式a2-2ab+b2-c2的值( )A、大于零 B、等于零 C、小于零 D、不能确定10. 小明坐滴滴打车前去火车高铁站,小明可以选择两条不同路线:路线A的全程是25千米,但交通比较拥堵,路线B的全程比路线A的全程多7千米,但平均车速比走路线A时能提高60%,若走路线B的全程能比走路线A少用15分钟.若设走路线A时的平均速度为x千米/小时,根据题意,可列分式方程( )
A、 =15 B、 =15 C、 = D、 =11. 如图,∠AOB=60°,点P是∠AOB内的定点且OP= ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )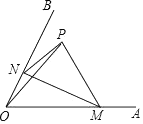 A、 B、 C、6 D、312. 如图,已知△ ABC中,AB=AC,∠BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ABC内绕顶点P旋转时(点E与A,B重合).上述结论中始终正确的有( )
A、 B、 C、6 D、312. 如图,已知△ ABC中,AB=AC,∠BAC=90°,直角∠ EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:①AE=CF;②△EPF是等腰直角三角形; ③2S四边形AEPF=S△ ABC; ④BE+CF=EF.当∠ EPF在△ABC内绕顶点P旋转时(点E与A,B重合).上述结论中始终正确的有( )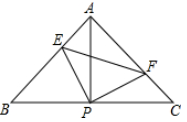 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知(x+y)2=25,(x﹣y)2=9,则x2+y2= .14. 当x时,分式 的值为正.15. 小明从P点出发,沿直线前进10米后向右转α,接着沿直线前进10米,再向右转α, ,照这样走下去,第一次回到出发地点P时,一共走了120米,则α的度数是 .
 16. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.做法中用到全等三角形判定的依据是.
16. 工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC即是∠AOB的平分线.做法中用到全等三角形判定的依据是.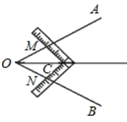 17. 如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为。
17. 如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠EFC′=120°,那么∠ABE的度数为。 18. 如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4 , …若∠A=70°,则锐角∠An的度数为.
18. 如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4 , …若∠A=70°,则锐角∠An的度数为.
三、解答题
-
19. 解方程: .20. 因式分解:(1)、–a4+16;(2)、21. 先化简 ,再从﹣1、2、3、4中选一个合适的数作为x的值代入求值.22. 按要求作图:已知A(﹣2,1),B(﹣1,2),C(﹣3,4).
 (1)、画出与三角形ABC关于y轴对称的三角形A1B1C1;(2)、将三角形A1B1C1先向右平移2个单位,再向下平移1个单位,得到三角形A2B2C2 , 则三角形A2B2C2顶点坐标分别为:A2B2C2;(3)、若点P(a-1,b+2)与点A关于x轴对称,则a= , b= .23. 如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H.
(1)、画出与三角形ABC关于y轴对称的三角形A1B1C1;(2)、将三角形A1B1C1先向右平移2个单位,再向下平移1个单位,得到三角形A2B2C2 , 则三角形A2B2C2顶点坐标分别为:A2B2C2;(3)、若点P(a-1,b+2)与点A关于x轴对称,则a= , b= .23. 如图,在Rt△ABC中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P点作PF⊥AD交BC的延长线于点F,交AC于点H. (1)、∠APB的度数为°;(2)、求证:△ABP≌△FBP;(3)、求证:AH+BD=AB.24. 为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.(1)、求签字笔和笔记本的单价分别是多少元?(2)、为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类图书,如果给每名获奖同学都买一本图书,需要花费720元;书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠.学校如果多买12本,则可以享受优惠且所花钱数与原来相同.问学校获奖的同学有多少人?25.
(1)、∠APB的度数为°;(2)、求证:△ABP≌△FBP;(3)、求证:AH+BD=AB.24. 为弘扬中华民族传统文化,某校举办了“古诗文大赛”,并为获奖同学购买签字笔和笔记本作为奖品.1支签字笔和2个笔记本共8.5元,2支签字笔和3个笔记本共13.5元.(1)、求签字笔和笔记本的单价分别是多少元?(2)、为了激发学生的学习热情,学校决定给每名获奖同学再购买一本文学类图书,如果给每名获奖同学都买一本图书,需要花费720元;书店出台如下促销方案:购买图书总数超过50本可以享受8折优惠.学校如果多买12本,则可以享受优惠且所花钱数与原来相同.问学校获奖的同学有多少人?25.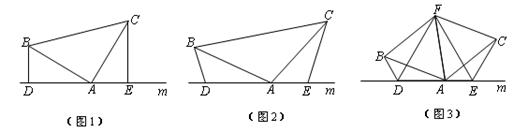 (1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
(1)、如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.(2)、如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC= ,其中 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)、拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.