2017年重庆市普通高等学校高考数学预测卷（理科）（3）

试卷更新日期：2017-08-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 在复平面内，复数 $\frac{10 i}{3 + i}$ 的共轭复数对应的点坐标为（）

A、（1，3） B、（1，﹣3） C、（﹣1，3） D、（﹣1，﹣3）

查看试题解析
2. 设集合M={x|y= $\sqrt{l o g_{\frac{1}{2}} x - 1}$ }，N={x||x﹣ $\frac{1}{2}$ |≤ $\frac{1}{4}$ }，则M∩N=（）

A、[2，+∞） B、[﹣1， $\frac{3}{4}$ ] C、[ $\frac{1}{4}$ ， $\frac{1}{2}$ ] D、[ $\frac{1}{4}$ ， $\frac{3}{4}$ ]

查看试题解析
3. 过坐标原点O作单位圆x²+y²=1的两条互相垂直的半径OA、OB，若在该圆上存在一点C，使得 $\vec{O C}$ =a $\vec{O A}$ +b $\vec{O B}$ （a、b∈R），则以下说法正确的是（）

A、点P（a，b）一定在单位圆内 B、点P（a，b）一定在单位圆上 C、点P（a，b）一定在单位圆外 D、当且仅当ab=0时，点P（a，b）在单位圆上

查看试题解析
4. 已知圆C₁：（x+1）²+（y﹣1）²=4，圆C₂与圆C₁关于直线x﹣y﹣1=0对称，则圆C₂的方程为（）

A、（x+2）²+（y﹣2）²=4 B、（x﹣2）²+（y+2）²=4 C、（x+2）²+（y+2）²=4 D、（x﹣2）²+（y﹣2）²=4

查看试题解析
5. 设三位数n=100a+10b+c，若以a，b，c∈{1，2，3，4}为三条边的长可以构成一个等腰（含等边）三角形，则这样的三位数n有（　　）

A、12种 B、24种 C、28种 D、36种

查看试题解析
6. 某几何体的三视图如图所示，则该几何体的外接球的表面积为（）

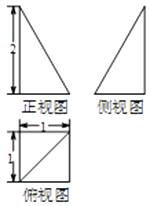A、24π B、12π C、8π D、6π

查看试题解析
7. 函数y=sin（2x+φ）的图象沿x轴向左平移 $\frac{π}{8}$ 个单位后，得到一个偶函数的图象，则φ的一个可能的值为（）

A、 $\frac{3 π}{4}$ B、 $\frac{π}{4}$ C、0 D、 $- \frac{π}{4}$

查看试题解析
8. 若如图框图所给的程序运行结果为S=28，那么判断框中应填入的关于k的条件是（）

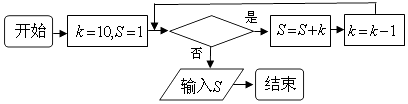A、k≥8 B、k＞8 C、k≥7 D、k＞9

查看试题解析
9. 已知θ是第三象限角，且sin⁴θ+cos⁴θ= $\frac{5}{9}$ ，那么sin2θ等于（）

A、 $\frac{2 \sqrt{2}}{3}$ B、 $- \frac{2 \sqrt{2}}{3}$ C、 $\frac{2}{3}$ D、 $- \frac{2}{3}$

查看试题解析
10. 一袋中装有大小相同，编号分别为1，2，3，4，5，6，7，8的八个球，从中有放回地每次取一个球，共取2次，则取得两个球的编号和不小于15的概率为（）

A、 $\frac{1}{32}$ B、 $\frac{1}{64}$ C、 $\frac{3}{32}$ D、 $\frac{3}{64}$

查看试题解析
11. 从双曲线 $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的左焦点F引圆x²+y²=a²的切线，切点为T，延长FT交双曲线右支于P点，若M为线段FP的中点，O为坐标原点，则|MO|﹣|MT|等于（）

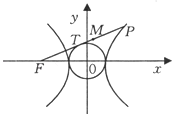A、c﹣a B、b﹣a C、a﹣b D、c﹣b

查看试题解析
12. 若函数f（x）=x²+ax+ $\frac{1}{x}$ 在（ $\frac{1}{2}$ ，+∞）上是增函数，则a的取值范围是（）

A、[﹣1，0] B、[﹣1，+∞） C、[0，3] D、[3，+∞）

查看试题解析

二、填空题

13. 在△ABC中，角A、B、C所对的边分别是a、b、c，若b= $\sqrt{2}$ asinB，则角A的大小为．

查看试题解析
14. 下列四个结论中假命题的序号是．
①垂直于同一直线的两条直线互相平行；
②平行于同一直线的两直线平行；
③若直线a，b，c满足a∥b，b⊥c，则a⊥c；
④若直线a，b是异面直线，则与a，b都相交的两条直线是异面直线．

查看试题解析
15. 已知实数x，y满足不等式组 ${\begin{matrix} 2 x - 3 y + 6 \geq 0 \\ 2 x + y - 2 \leq 0 \\ y + 1 \geq 0 \end{matrix}$ ，则z=|x|+y的取值范围为．

查看试题解析
16. 设f（x）是定义在R上的奇函数，且对任意实数x，恒有f（x+2）=﹣f（x）．当x∈[0，2]时，f（x）=2x﹣x² ．当x∈[2，4]时，则f（x）= ．

查看试题解析

三、解答题

17. 数列{a_n}满足a_n=3a_n_﹣₁+3ⁿ﹣1（n∈N^* ， n≥2），
已知a₃=95．

(1)、求a₁ ， a₂；

(2)、是否存在一个实数t，使得 $b_{n} = \frac{1}{3^{n}} (a_{n} + t) (n \in N^{*})$ ，且{b_n}为等差数列？若存在，则求出t的值；若不存在，请说明理由．

查看试题解析
18. 某工厂生产甲，乙两种芯片，其质量按测试指标划分为：指标大于或等于82为合格品，小于82为次品．现随机抽取这两种芯片各100件进行检测，检测结果统计如表：
测试指标
[70，76）
[76，82）
[82，88）
[88，94）
[94，100]
芯片甲
8
12
40
32
8
芯片乙
7
18
40
29
6
（Ⅰ）试分别估计芯片甲，芯片乙为合格品的概率；
（Ⅱ）生产一件芯片甲，若是合格品可盈利40元，若是次品则亏损5元；生产一件芯片乙，若是合格品可盈利50元，若是次品则亏损10元．在（I）的前提下，
（i）记X为生产1件芯片甲和1件芯片乙所得的总利润，求随机变量X的分布列和数学期望；
（ii）求生产5件芯片乙所获得的利润不少于140元的概率．

查看试题解析
19. 如图，四棱锥P﹣ABCD的底面ABCD是正方形，PD⊥平面ABCD，E为PB上的点，且2BE=EP．

(1)、证明：AC⊥DE；

(2)、若PC= $\sqrt{2}$ BC，求二面角E﹣AC﹣P的余弦值．

查看试题解析
20. 已知椭圆C₁的方程为 $\frac{x^{2}}{4}$ + $\frac{y^{2}}{2}$ =1，双曲线C₂的左、右焦点分别是C₁的左、右顶点，而以双曲线C₂的左、右顶点分别是椭圆C₁的左、右焦点．

(1)、求双曲线C₂的方程；

(2)、记O为坐标原点，过点Q（0，2）的直线l与双曲线C₂相交于不同的两点E、F，若△OEF的面积为2 $\sqrt{2}$ ，求直线l的方程．

查看试题解析
21. 已知函数f（x）=me^x﹣lnx﹣1．

(1)、当m=1，x∈[1，+∞）时，求y=f（x）的值域；

(2)、当m≥1时，证明：f（x）＞1．

查看试题解析
22. 在极坐标系中，圆C的极坐标方程为：ρ²=4ρ（cosθ+sinθ）﹣3．若以极点O为原点，极轴所在直线为x轴建立平面直角坐标系．
（Ⅰ）求圆C的参数方程；
（Ⅱ）在直角坐标系中，点P（x，y）是圆C上动点，试求x+2y的最大值，并求出此时点P的直角坐标．

查看试题解析
23. 已知函数f（x）=|x+2|+|x﹣1|．

(1)、求不等式f（x）＞5的解集；

(2)、若对于任意的实数x恒有f（x）≥|a﹣1|成立，求实数a的取值范围．

查看试题解析

测试指标	[70，76）	[76，82）	[82，88）	[88，94）	[94，100]
芯片甲	8	12	40	32	8
芯片乙	7	18	40	29	6