2017年重庆市普通高等学校高考数学预测卷（理科）（1）

试卷更新日期：2017-08-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知集合A={x|x²+x﹣6＜0}，B={y|y=2^x﹣1，x≤2}，则A∩B=（）

A、（﹣3，3] B、（﹣1，3） C、（﹣3，2] D、（﹣1，2）

查看试题解析
2. 复数z满足z（2+i）=3﹣6i（i为虚数单位），则复数z的虚部为（）

A、3 B、﹣3 C、3i D、﹣3i

查看试题解析
3.
如图，在△OAB，点P在边AB上，且AP：PB=5：3，则 $\vec{O P}$ =（）

A、 $\frac{5}{8} \vec{O B}$ + $\frac{3}{8} \vec{O A}$ B、 $\frac{5}{8} \vec{O A}$ + $\frac{3}{8} \vec{O B}$ C、 $\frac{5}{8} \vec{O B}$ ﹣ $\frac{3}{8} \vec{O A}$ D、 $\frac{5}{8} \vec{O A}$ ﹣ $\frac{3}{8} \vec{O B}$

查看试题解析
4. 正数a、m、b构成公差为﹣ $\frac{1}{2}$ 的等差数列，a，b的等比中项是2 $\sqrt{5}$ ，则双曲线 $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1的离心率为（）

A、 $\frac{5}{3}$ B、 $\frac{\sqrt{41}}{4}$ C、 $\frac{5}{4}$ D、 $\frac{\sqrt{41}}{5}$

查看试题解析
5. 某舞步每一节共九步，且每一步各不相同，其中动作A三步，动作B三步，动作C三步，同一种动作相邻，则这种舞步一节中共有多少种不同的变化（）

A、1296种 B、216种 C、864种 D、1080种

查看试题解析
6. 一个几何体的三视图如图所示，则该几何体的表面积为（）

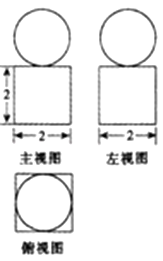A、4π+8 B、 $\frac{4 π}{3}$ +24 C、4π+24 D、 $\frac{4 π}{3}$ +8

查看试题解析
7. 函数f（x）=sin²x+sinxcosx+1的最小正周期是（）

A、2π B、π C、 $\frac{3}{2}$ π D、 $\frac{1}{2}$ π

查看试题解析
8. 某程序框图如图所示，现将输出（x，y）值依次记为：（x₁ ， y₁），（x₂ ， y₂），…，（x_n ， y_n），…，若程序运行中输出一个数组是（x，﹣10），则数组中的x=（）

A、16 B、32 C、64 D、128

查看试题解析
9. 已知f（x）是定义在（0，3）上的函数，f（x）的图象如图所示，那么不等式f（x）cosx＜0的解集是（）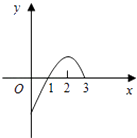

A、（0，1）∪（2，3） B、 $(1 ， \frac{π}{2}) \cup^{} (\frac{π}{2} ， 3)$ C、 $(0 ， 1) \cup^{} (\frac{π}{2} ， 3)$ D、（0，1）∪（1，3）

查看试题解析
10. 连续投掷两次骰子得到的点数分别为m，n，向量 $\vec{a} = (m ， n)$ 与向量 $\vec{b} = (1 ， 0)$ 的夹角记为α，则α $\in (0 ， \frac{π}{4})$ 的概率为（）

A、 $\frac{5}{18}$ B、 $\frac{5}{12}$ C、 $\frac{1}{2}$ D、 $\frac{7}{12}$

查看试题解析
11. 已知抛物线C的顶点在坐标原点，焦点为F（1，0），直线l与抛物线C相交于A、B两点，若AB的中点为（2，2），则直线的斜率为（）

A、2 B、﹣2 C、1 D、﹣1

查看试题解析
12. 定义在R上的函数f（x）满足f（x+6）=f（x），当﹣3≤x＜﹣1时，f（x）=﹣（x+2）²；当﹣1≤x＜3时，f（x）=x，则f（1）+f（2）+f（3）+…+f（2017）=（）

A、337 B、338 C、1678 D、2012

查看试题解析

二、填空题

13. 在△ABC中，已知面积S= $\frac{1}{4}$ （a²+b²﹣c²），则角C的度数为．

查看试题解析
14. 已知α，β是两个不同的平面，m，n是两条不同的直线，给出下列命题：

①若m⊥α，m⊂β，则α⊥β；
②若m⊂α，n⊂α，m∥β，n∥β，则α∥β；
③若α∩β=m，n∥m，且n⊄α，n⊄β，则n∥α且n∥β
其中正确命题的序号是．

查看试题解析
15. 已知实数x，y满足 ${\begin{matrix} 4 x + y - 9 \geq 0 \\ x - y - 1 \leq 0 \\ y \leq 3 \end{matrix}$ ，则z=x﹣3y的最大值是．

查看试题解析
16. 已知函数f（x）是R上的偶函数，且在（﹣∞，0]上是减函数，若f（a）≥f（2），则实数a的取值范围是．

查看试题解析

三、解答题

17. 已知数列{a_n}中，a₁₀=17，其前n项和S_n满足S_n=n²+cn+2．

(1)、求实数c的值；

(2)、求数列{a_n}的通项公式．

查看试题解析
18. 为了回馈顾客，某商场在元旦期间举行购物抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为 $\frac{3}{5}$ ，中奖可以获得3分；方案乙的中奖率为 $\frac{3}{4}$ ，中奖可以获得2分；未中奖则不得分，每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，抽奖结束后凭分数兑换奖品．

(1)、若小明选择方案甲抽奖，小红选择方案乙抽奖，记他们的累计得分为X，求X≥3的概率；

(2)、若小明、小红两人都选择方案甲或都选择方案乙进行抽奖，分别求两种方案下小明、小红累计得分的分布列，并指出为了累计得分较大，两种方案下他们选择何种方案较好，并给出理由？

查看试题解析
19. 如图，四棱锥P﹣ABCD中，底面ABCD是平行四边形，∠ACB=90°，平面PAD⊥平面ABCD，PA=BC=1，PD=AB= $\sqrt{2}$ ，E、F分别为线段PD和BC的中点．
（Ⅰ）求证：CE∥平面PAF；
（Ⅱ）在线段BC上是否存在一点G，使得平面PAG和平面PGC所成二面角的大小为60°？若存在，试确定G的位置；若不存在，请说明理由．

查看试题解析
20. 已知点P（x，y）是曲线C上任意一点，点（x，2y）在圆x²+y²=8上，定点M（2，1），平行于OM的直线l在y轴上的截距为m（m≠0），直线l与曲线C交于A、B两个不同点．

(1)、求曲线C的方程；

(2)、求证直线MA、MB与x轴始终围成一个等腰三角形．

查看试题解析
21. 已知函数f（x）=g（x）﹣（a﹣1）lnx，g（x）=ax+ $\frac{2 a - 1}{x}$ +1﹣3a+（a﹣1）lnx．

(1)、当a=1时，求函数y=f（x）在点（2，f（2））处的切线方程；

(2)、若不等式g（x）≥0在x∈[1，+∞）时恒成立，求正实数a的取值范围．

查看试题解析
22. 已知曲线C： ${\begin{matrix} x = 2 c o s θ \\ y = 3 s i n θ \end{matrix}$ ，（θ为参数），在以O为极点，x轴正半轴为极轴的极坐标系中，直线l的极坐标方程2ρcosθ+ρsinθ﹣6=0．

(1)、写出曲线C的普通方程，直线l的直角坐标方程；

(2)、过曲线C上任意一点P作与l夹角为30°的直线，交l于点A，求|PA|的最大值与最小值．

查看试题解析
23. 已知函数f（x）=|2x﹣a|+|x﹣1|．

(1)、当a=3时，求不等式f（x）≥2的解集；

(2)、若f（x）≥5﹣x对∀x∈R恒成立，求实数a的取值范围．

查看试题解析