2017年浙江省温州市普通高中高考数学模拟试卷(4月份)
试卷更新日期:2017-08-12 类型:高考模拟
一、选择题
-
1. 设集合A={x∈R|x>0},B={x∈R|x2≤1},则A∩B=( )A、(0,1) B、(0,1] C、[﹣1,1] D、[﹣1,+∞)2. 设复数z= ,其中i为虚数单位,则|z|=( )A、1 B、 C、2 D、33. “平面α内的两条直线与平面β都平行”是“平面α与平面β平行”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 设(1+x)6=a0+a1x+a2x2+…+a6x6 , 其中x、ai∈R,i=0,1,…,6,则a1+a3+a5=( )A、16 B、32 C、64 D、1285. 函数y=xsinx(x∈[﹣π,π])的图象可能是( )A、
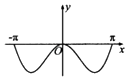 B、
B、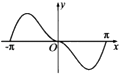 C、
C、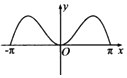 D、
D、 6. 已知实数x,y满足 ,则|3x+y|的最大值为( )A、5 B、6 C、7 D、87. 在四面体ABCD中,二面角A﹣BC﹣D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( )
6. 已知实数x,y满足 ,则|3x+y|的最大值为( )A、5 B、6 C、7 D、87. 在四面体ABCD中,二面角A﹣BC﹣D为60°,点P为直线BC上一动点,记直线PA与平面BCD所成的角为θ,则( ) A、θ的最大值为60° B、θ的最小值为60° C、θ的最大值为30° D、θ的最小值为30°8. 设 , , 均为非零向量,若|( + )• |=|( ﹣ )• |,则( )A、 ∥ B、 ⊥ C、 ∥ 或 ∥ D、 ⊥ 或 ⊥9. 给定R上的函数f(x),( )A、存在R上函数g(x),使得f(g(x))=x B、存在R上函数g(x),使得g(f(x))=x C、存在R上函数g(x),使得f(g(x))=g(x) D、存在R上函数g(x),使得f(g(x))=g(f(x))10. 设P为椭圆C: + =1(a>b>0)上的动点,F1、F2为椭圆C的焦点,I为△PF1F2的内心,则直线IF1和直线IF2的斜率之积( )
A、θ的最大值为60° B、θ的最小值为60° C、θ的最大值为30° D、θ的最小值为30°8. 设 , , 均为非零向量,若|( + )• |=|( ﹣ )• |,则( )A、 ∥ B、 ⊥ C、 ∥ 或 ∥ D、 ⊥ 或 ⊥9. 给定R上的函数f(x),( )A、存在R上函数g(x),使得f(g(x))=x B、存在R上函数g(x),使得g(f(x))=x C、存在R上函数g(x),使得f(g(x))=g(x) D、存在R上函数g(x),使得f(g(x))=g(f(x))10. 设P为椭圆C: + =1(a>b>0)上的动点,F1、F2为椭圆C的焦点,I为△PF1F2的内心,则直线IF1和直线IF2的斜率之积( ) A、是定值 B、非定值,但存在最大值 C、非定值,但存在最小值 D、非定值,且不存在最值
A、是定值 B、非定值,但存在最大值 C、非定值,但存在最小值 D、非定值,且不存在最值二、填空题
-
11. 圆x2+y2﹣2y﹣3=0的圆心坐标是 , 半径 .12. 已知某几何体的三视图如图所示(单位:cm),则此几何体的体积为 , 表面积为 .
 13. 在△ABC中,内角A、B、C所对的边长分别为a、b、c,记S为△ABC的面积,若A=60°,b=1,S= ,则c= , cosB= .14. 袋中有6个编号不同的黑球和3个编号不同的白球,这9个球的大小及质地都相同,现从该袋中随机摸取3个球,则这三个球中恰有两个黑球和一个白球的方法总数是 , 设摸取的这三个球中所含的黑球数为X,则P(X=k)取最大值时,k的值为 .15. 若关于x的不等式|x|+|x+a|<b的解集为(﹣2,1),则实数对(a,b)= .16. 已知等差数列{an}满足:a4>0,a5<0,则满足 >2的n的集合是 .17. 已知函数f(x)=x2+ax+b(a、b∈R)在区间[0,1]上有零点,则ab的最大值是 .
13. 在△ABC中,内角A、B、C所对的边长分别为a、b、c,记S为△ABC的面积,若A=60°,b=1,S= ,则c= , cosB= .14. 袋中有6个编号不同的黑球和3个编号不同的白球,这9个球的大小及质地都相同,现从该袋中随机摸取3个球,则这三个球中恰有两个黑球和一个白球的方法总数是 , 设摸取的这三个球中所含的黑球数为X,则P(X=k)取最大值时,k的值为 .15. 若关于x的不等式|x|+|x+a|<b的解集为(﹣2,1),则实数对(a,b)= .16. 已知等差数列{an}满足:a4>0,a5<0,则满足 >2的n的集合是 .17. 已知函数f(x)=x2+ax+b(a、b∈R)在区间[0,1]上有零点,则ab的最大值是 .三、解答题
-
18. 已知函数f(x)= cos2x﹣2cos2(x+ )+1.
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)求f(x)在区间[0, ]上的最值.
19. 如图,三棱柱ABC﹣A1B1C1所有的棱长均为2,A1B= ,A1B⊥AC.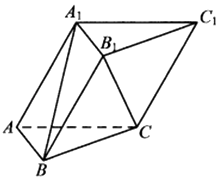
(Ⅰ)求证:A1C1⊥B1C;
(Ⅱ)求直线AC和平面ABB1A1所成角的余弦值.
20. 设函数f(x)=4x3+ ,x∈[0,1],证明:(Ⅰ)f(x)≥1﹣2x+3x2;
(Ⅱ) <f(x)≤ .
