2017年四川省内江市高考数学五模试卷（理科）

试卷更新日期：2017-08-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 设集合A={x∈Z|x²＜3}，B={x|x＞﹣1}，则A∩B=（）

A、{0，1} B、{﹣1，0} C、{﹣1，0，1} D、{0，1，2}

查看试题解析
2. 设z=1﹣i（i为虚数单位），若复数 $\frac{2}{z}$ ﹣z²在复平面内对应的向量为 $\vec{O Z}$ ，则向量 $\vec{O Z}$ 的模是（）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{5}$ D、 $\sqrt{10}$

查看试题解析
3. 已知向量 $\vec{a}$ =（1，﹣2）， $\vec{b}$ =（1，1）， $\vec{m}$ = $\vec{a}$ + $\vec{b}$ ， $\vec{n}$ = $\vec{a}$ ﹣λ $\vec{b}$ ，如果 $\vec{m}$ ⊥ $\vec{n}$ ，那么实数λ=（）

A、4 B、3 C、2 D、1

查看试题解析
4. 在正项等比数列{a_n}中，a₁₀₀₈a₁₀₁₀= $\frac{1}{100}$ ，则lga₁+lga₂+…+lga₂₀₁₇=（）

A、﹣2016 B、﹣2017 C、2016 D、2017

查看试题解析
5. 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题：“今有垣厚十尺，两鼠对穿，初日各一尺，大鼠日自倍，小鼠日自半，问几何日相逢？”现用程序框图描述，如图所示，则输出结果n=（）

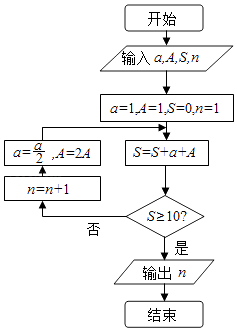A、4 B、5 C、2 D、3

查看试题解析
6. 某校开设A类选修课3门，B类选修课3门，一位同学从中选3门．若要求两类课程中各至少选一门，则不同的选法共有（）

A、3种 B、6种 C、9种 D、18种

查看试题解析
7. 已知随机变量ξ服从正态分布N（1，1），若P（ξ＜3）=0.977，则P（﹣1＜ξ＜3）=（）

A、0.683 B、0.853 C、0.954 D、0.977

查看试题解析
8. 如图，已知三棱锥P﹣ABC的底面是等腰直角三角形，且∠ACB= $\frac{π}{2}$ ，侧面PAB⊥底面ABC，AB=PA=PB=2．则这个三棱锥的三视图中标注的尺寸x，y，z分别是（）

A、 $\sqrt{3}$ ，1， $\sqrt{2}$ B、 $\sqrt{3}$ ，1，1 C、2，1， $\sqrt{2}$ D、2，1，1

查看试题解析
9. 已知：
命题p：若函数f（x）=x²+|x﹣a|是偶函数，则a=0．
命题q：∀m∈（0，+∞），关于x的方程mx²﹣2x+1=0有解．
在①p∨q；②p∧q；③（￢p）∧q；④（￢p）∨（￢q）中为真命题的是（）

A、②③ B、②④ C、③④ D、①④

查看试题解析
10. 已知实数x，y满足 ${\begin{matrix} x - 4 y \leq - 3 \\ 3 x + 5 y \leq 25 \\ x \geq 1 \end{matrix}$ ，记z=ax﹣y（其中a＞0）的最小值为f（a），若f（a）≥﹣ $\frac{2}{5}$ ，则实数a的最小值为（）

A、3 B、4 C、5 D、6

查看试题解析
11. 已知双曲线C： $\frac{x^{2}}{a^{2}}$ ﹣ $\frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）点有顶点A，O为坐标原点，以A为圆心与双曲线C的一条渐近线交于两点P，Q，若∠PAQ=60°且 $\vec{O Q}$ =2 $\vec{O P}$ ，则双曲线C的离心率为（）

A、 $\frac{\sqrt{39}}{6}$ B、 $\frac{2 \sqrt{3}}{3}$ C、 $\frac{\sqrt{7}}{2}$ D、 $\sqrt{3}$

查看试题解析
12. 已知函数f（x）= ${\begin{matrix} l o g_{4} (x + 1) + x - 1 (x > 0) \\ x - {(\frac{1}{4})}^{x + 1} + 3 (x \leq 0) \end{matrix}$ ，若f（x）的两个零点分别为x₁ ， x₂ ，则|x₁﹣x₂|=（）

A、 $\sqrt{2}$ B、1+ $\frac{\sqrt{2}}{2}$ C、2 D、 $\frac{3}{2}$ +ln2

查看试题解析

二、填空题

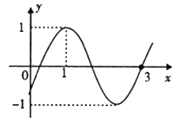
13. （x+y）（x﹣y）⁷点展开式中x⁴y⁴的系数为（用数字填写答案）

查看试题解析
14. 已知函数f（x）=sin（ωx+φ）（ω＞0）的图象如图所示，则f（4）= ．

查看试题解析
15. 已知三被锥S﹣ABC的体积为 $\frac{4 \sqrt{5}}{3}$ ，底面△ABC是边长为2的正三角形，且所有頂点都在直径为SC的球面上．则此球的半径为．

查看试题解析
16. 已知数列{a_n}的首项a₁=1，且满足a_n₊₁﹣a_n≤n•2ⁿ ， a_n﹣a_n₊₂≤﹣（3n+2）•2ⁿ ，则a₂₀₁₇= ．

查看试题解析

三、解答题

17. 某工厂为了解用电量y与气温x℃之间的关系，随机统计了5天的用电量与当天气温，得到如下统计表：
曰期
8月1曰
8月7日
8月14日
8月18日
8月25日
平均气温（℃）
33
30
32
30
25
用电量（万度）
38
35
41
36
30
$\sum_{i = 1}^{5}$ x_iy_i=5446， $\sum_{i = 1}^{5}$ x_i²=4538， $\hat{b}$ = $\frac{\sum_{i = 1}^{5} x_{i} y_{i} - 5 \bar{x} \bar{y}}{\sum_{i = 1}^{5} x_{i}^{2} - 5 {\bar{x}}^{2}}$ ， $\hat{a}$ = $\bar{y}$ ﹣ $\hat{b} \bar{x}$

(1)、请根据表中的数据，求出y关于x的线性回归方程．据气象預报9月3日的平均气温是 23℃，请预测9月3日的用电量；（结果保留整数）

(2)、请从表中任选两天，记用电量（万度）超过35的天数为ξ，求ξ的概率分布列，并求其数学期望和方差．

查看试题解析
18. 如图，D是直角△ABC斜边BC上一点，AC= $\sqrt{3}$ DC．

(1)、若∠DAC=30°，求角B的大小；

(2)、若BD=2DC，且AD=3 $\sqrt{2}$ ，求DC的长．

查看试题解析
19. 如图，已知四边形ABCD是正方形，EA⊥平面ABCD，PD∥EA，AD=PD=2EA=2，F，G，H分别为BP，BE，PC的中点．

(1)、求证：GH∥平面ADPE；

(2)、M是线段PC上一点，且PM= $\frac{3 \sqrt{2}}{2}$ ，求二面角C﹣EF﹣M的余弦值．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）过点（ $\sqrt{2}$ ，1），且焦距为2 $\sqrt{2}$ ．

(1)、求椭圆C的方程；

(2)、若直线l：y=k（x+1）（k＞﹣2）与椭圆C相交于不同的两点A、B，线段AB的中点M到直线2x+y+t=0的距离为 $\frac{3 \sqrt{5}}{5}$ ，求t（t＞2）的取值范围．

查看试题解析
21. 已知函数f（x）=xe^x﹣lnx（ln2≈﹣0.693， $\sqrt{e}$ ≈1.648，均为不足近似值）

(1)、当x≥1时，判断函数f（x）的单调性；

(2)、证明：当x＞0时，不等式f（x）＞ $\frac{27}{20}$ 恒成立．

查看试题解析
22. 已知在平面直角坐标系xOy中，过点P（1，0）的直线l的参数方程是 ${\begin{matrix} x = \frac{\sqrt{3}}{2} t + 1 \\ y = \frac{1}{2} t \end{matrix}$ （t是参数），以原点O为极点，x轴正半轴为极轴建立极坐标系，曲线C点的极坐标方程为ρ=﹣4sin（θ﹣ $\frac{π}{6}$ ）．

(1)、判断直线l与曲线C的位置关系；

(2)、若直线l与曲线C交于两点A、B，求|PA|•|PB|的值．

查看试题解析
23. 已知函数f（x）=|x+2|﹣2|x+1|．

(1)、求f（x）的最大值；

(2)、若存在x∈[﹣2，1]使不等式a+1＞f（x）成立，求实数a的取值范围．

查看试题解析

曰期	8月1曰	8月7日	8月14日	8月18日	8月25日
平均气温（℃）	33	30	32	30	25
用电量（万度）	38	35	41	36	30