2017年四川省眉山市仁寿一中高考数学三模试卷(理科)
试卷更新日期:2017-08-12 类型:高考模拟
一、选择题
-
1. 已知全集U={1,2,3,4,5},M={3,4,5},N={2,3},则集合(∁UN)∩M=( )A、{2} B、{1,3} C、{2,5} D、{4,5}2. 已知i是虚数单位,复数 的虚部为( )A、 B、﹣ C、 i D、﹣ i3. 已知两条直线m,n和两个不同平面α,β,满足α⊥β,α∩β=l,m∥α,n⊥β,则( )A、m∥n B、m⊥n C、m∥l D、n⊥l4. 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
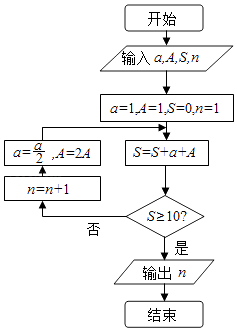 A、4 B、5 C、2 D、35. 函数 f(x)= 的大致图象是( )A、
A、4 B、5 C、2 D、35. 函数 f(x)= 的大致图象是( )A、 B、
B、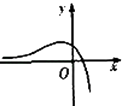 C、
C、 D、
D、 6. 记等比数列{an}的前n项和为Sn , 若S3=2,S6=18,则 等于( )A、﹣3 B、5 C、﹣31 D、337. 2位男生和3位女生共5位同学站成一排,则3位女生中有且只有两位女生相邻的概率是( )A、 B、 C、 D、8. 已知圆C:(x﹣ )2+(y﹣1)2=1和两点A(﹣t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )A、( , ) B、( , ) C、( , ) D、( , )9. 已知函数f(x)= sin(ωx+φ)(ω>0,﹣ <φ< ),A( ,0)为f(x)图象的对称中心,B,C是该图象上相邻的最高点和最低点,若BC=4,则f(x)的单调递增区间是( )A、(2k﹣ ,2k+ ),k∈Z B、(2kπ﹣ π,2kπ+ π),k∈Z C、(4k﹣ ,4k+ ),k∈Z D、(4kπ﹣ π,4kπ+ π),k∈Z10. 某几何体的三视图如图所示,则该几何体的体积为( )
6. 记等比数列{an}的前n项和为Sn , 若S3=2,S6=18,则 等于( )A、﹣3 B、5 C、﹣31 D、337. 2位男生和3位女生共5位同学站成一排,则3位女生中有且只有两位女生相邻的概率是( )A、 B、 C、 D、8. 已知圆C:(x﹣ )2+(y﹣1)2=1和两点A(﹣t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则当t取得最大值时,点P的坐标是( )A、( , ) B、( , ) C、( , ) D、( , )9. 已知函数f(x)= sin(ωx+φ)(ω>0,﹣ <φ< ),A( ,0)为f(x)图象的对称中心,B,C是该图象上相邻的最高点和最低点,若BC=4,则f(x)的单调递增区间是( )A、(2k﹣ ,2k+ ),k∈Z B、(2kπ﹣ π,2kπ+ π),k∈Z C、(4k﹣ ,4k+ ),k∈Z D、(4kπ﹣ π,4kπ+ π),k∈Z10. 某几何体的三视图如图所示,则该几何体的体积为( )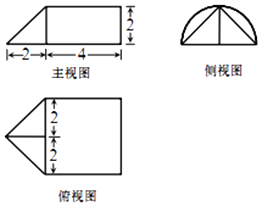 A、 +8π B、 +8π C、 +16π D、 +16π11. 已知双曲线E: ﹣ =1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=6,P是E右支上一点,PF1与y轴交于点A,△PAF2的内切圆在边AF2上的切点为Q,若|AQ|= ,则E的离心率是( )A、2 B、 C、 D、12. 定义在R上的函数f(x)的导函数为f′(x),f(0)=0.若对任意x∈R,都有f(x)>f′(x)+1,则使得f(x)+ex<1成立的x的取值范围为( )A、(﹣∞,0) B、(﹣∞,1) C、(﹣1,+∞) D、(0,+∞)
A、 +8π B、 +8π C、 +16π D、 +16π11. 已知双曲线E: ﹣ =1(a>0,b>0)的左、右焦点分别为F1、F2 , |F1F2|=6,P是E右支上一点,PF1与y轴交于点A,△PAF2的内切圆在边AF2上的切点为Q,若|AQ|= ,则E的离心率是( )A、2 B、 C、 D、12. 定义在R上的函数f(x)的导函数为f′(x),f(0)=0.若对任意x∈R,都有f(x)>f′(x)+1,则使得f(x)+ex<1成立的x的取值范围为( )A、(﹣∞,0) B、(﹣∞,1) C、(﹣1,+∞) D、(0,+∞)二、填空题
-
13. 若不等式组满足 ,则z=2x+y的最大值为 .14. 在 的展开式中,x的系数为 . (用数字作答)15. △ABC的外接圆的圆心为O,半径为1,2 + + = ,且| |=| |,则向量 在 方向上的投影 .16. Sn为数列{an}的前n项和,已知 .则{an}的通项公式an= .
三、解答题
-
17. 在△ABC中,角A、B、C所对的边为a、b、c,且满足cos2A﹣cos2B=2cos(A﹣ )cos(A+ ).
(Ⅰ)求角B的值;
(Ⅱ)若b= ≤a,求2a﹣c的取值范围.
18. 由于当前学生课业负担较重,造成青少年视力普遍下降,现从某高中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如图:
(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(Ⅲ)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记ξ表示抽到“好视力”学生的人数,求ξ的分布列及数学期望.
19. 如图,在四棱锥P﹣ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.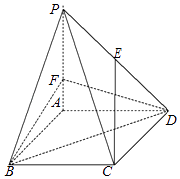
(Ⅰ)若 AF=1,求证:CE∥平面 BDF;
(Ⅱ)若 AF=2,求平面 BDF 与平面 PCD所成的锐二面角的余弦值.
20. 已知椭圆C: + =1(a>b>0)经过点(1, ),离心率为 ,点A为椭圆C的右顶点,直线l与椭圆相交于不同于点A的两个点P(x1 , y1),Q(x2 , y2).(Ⅰ)求椭圆C的标准方程;
(Ⅱ)当 ⊥ =0时,求△OPQ面积的最大值.
21. 设f(x)=xex(e为自然对数的底数),g(x)=(x+1)2 .(Ⅰ)记 ,讨论函数F(x)的单调性;
(Ⅱ)令G(x)=af(x)+g(x)(a∈R),若函数G(x)有两个零点,求实数a的取值范围.