2017年四川省大教育联盟高考数学三诊试卷（理科）

试卷更新日期：2017-08-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 已知全集U，集合M，N满足M⊆N⊆U，则下列结论正确的是（）

A、M∪N=U B、（∁_UM）∪（∁_UN）=U C、M∩（∁_UN）=∅ D、（∁_UM）∪（∁_UN）=∅

查看试题解析
2. 已知复数z满足（2+i）z=2﹣i（i为虚数单位），则z在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知α是锐角，若cos（α+ $\frac{π}{6}$ ）= $\frac{5}{13}$ ，则sin（α﹣ $\frac{π}{12}$ ）=（）

A、﹣ $\frac{17 \sqrt{2}}{26}$ B、﹣ $\frac{7 \sqrt{2}}{26}$ C、 $\frac{7 \sqrt{2}}{26}$ D、 $\frac{17 \sqrt{2}}{26}$

查看试题解析
4. 已知实数x，y满足不等式 ${\begin{matrix} x + y \leq 2 \\ 2 x + y \leq 3 \\ x \geq 0 \\ y \geq 0 \end{matrix}$ ，则3x+2y的最大值为（）

A、0 B、2 C、4 D、5

查看试题解析
5. 《九章算术》是我国古代内容极为丰富的数学名著，系统地总结了战国、秦、汉时期的数学成就．书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”，若某“阳马”的三视图如图所示（单位：cm），则该阳马的外接球的体积为（）

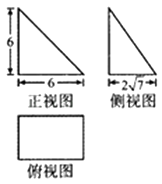A、100πcm³ B、 $\frac{500 π}{3} c m^{3}$ C、400πcm³ D、 $\frac{4000 π}{3} c m^{3}$

查看试题解析
6. 运行如图所示的程序，若输出y的值为1，则输入x的值为（）

A、0 B、0或﹣1 C、±1 D、1

查看试题解析
7. 设直角坐标平面内与两个定点A（﹣2，0），B（2，0）的距离之差的绝对值等于2的点的轨迹是E．过点B作与x轴垂直的直线l与曲线E交于C，D两点，则 $\vec{A C} \cdot \vec{B D}$ =（）

A、﹣9 B、﹣3 C、3 D、9

查看试题解析
8. 利用计算机产生120个随机正整数，其最高位数字（如：34的最高位数字为3，567的最高位数字为5）的频数分布图如图所示，若从这120个正整数中任意取出一个，设其最高位数字为d（d=1，2，…，9）的概率为P，下列选项中，最能反映P与d的关系的是（）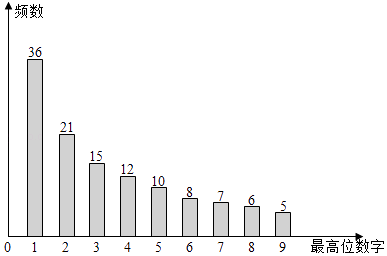

A、P=lg（1+ $\frac{1}{d}$ ） B、P= $\frac{1}{d + 2}$ C、P= $\frac{{(d - 5)}^{2}}{120}$ D、P= $\frac{3}{5}$ × $\frac{1}{2^{d}}$

查看试题解析
9. 已知ω为正整数，函数f（x）=sinωxcosωx+ $c o s^{2} ω x - \frac{1}{2}$ 在区间 $(- \frac{π}{3} ， \frac{π}{12})$ 内单调递增，则函数f（x）（）

A、最小值为 $- \frac{1}{2}$ ，其图象关于点 $(\frac{π}{4} ， 0)$ 对称 B、最大值为 $\frac{\sqrt{2}}{2}$ ，其图象关于直线 $x = - \frac{π}{8}$ 对称 C、最小正周期为2π，其图象关于点 $(\frac{3 π}{4} ， 0)$ 对称 D、最小正周期为π，其图象关于直线 $x = - \frac{3 π}{8}$ 对称

查看试题解析
10. 将正方形ABCD沿对角线BD折成直二面角后的图形如图所示，若E为线段BC的中点，则直线AE与平面ABD所成角的余弦为（）

A、 $\frac{1}{4}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{\sqrt{30}}{6}$ D、 $\frac{\sqrt{15}}{4}$

查看试题解析
11. 在直角梯形ABCD中，AB⊥AD，AD∥BC，AB=BC=2AD=2，E，F分别为BC，CD的中点，以A为圆心，AD为半径的半圆分别交BA及其延长线于点M，N，点P在 $\hat{M D N}$ 上运动（如图）．若 $\vec{A P} = λ \vec{A E} + μ \vec{B F}$ ，其中λ，μ∈R，则2λ﹣5μ的取值范围是（）

A、[﹣2，2] B、 $[- 2 ， 2 \sqrt{2}]$ C、 $[- 2 \sqrt{2} ， 2]$ D、 $[- 2 \sqrt{2} ， 2 \sqrt{2}]$

查看试题解析
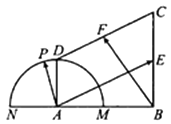12. 已知椭圆M： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的一个焦点为F（1，0），离心率为 $\frac{\sqrt{2}}{2}$ ，过点F的动直线交M于A，B两点，若x轴上的点P（t，0）使得∠APO=∠BPO总成立（O为坐标原点），则t=（）

A、2 B、 $\sqrt{2}$ C、 $- \sqrt{2}$ D、﹣2

查看试题解析

二、填空题

13. 从0，1，2，3，4五个数字中随机取两个数字组成无重复数字的两位数，则所得两位数为偶数的概率是．（结果用最简分数表示）

查看试题解析
14. 曲线y= $\sqrt{x}$ 和直线y=x围成的图形面积是．

查看试题解析
15. 在△ABC中，∠BAC=120°，AC=2AB=4，点D在BC上，且AD=BD，则AD= ．

查看试题解析
16. 已知函数f（x）=（x﹣1）e^x+ $\frac{1}{2} a x^{2} + 1$ （其中a∈R）有两个零点，则a的取值范围是．

查看试题解析

三、解答题

17. 已知数列{a_n}中，a₂=2，其前n项和S_n满足： $S_{n} = \frac{n (a_{n} - a_{1})}{2}$ （n∈N^*）．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）若 $b_{n} = n \cdot 2^{a_{n}}$ ，求数列{b_n}的前n项和T_n ．

查看试题解析
18. 第96届（春季）全国糖酒商品交易会于2017年3月23日至25日在四川举办．交易会开始前，展馆附近一家川菜特色餐厅为了研究参会人数与餐厅所需原材料数量的关系，查阅了最近5次交易会的参会人数x（万人）与餐厅所用原材料数量t（袋），得到如下数据：
第一次
第二次
第三次
第四次
第五次
参会人数x（万人）
11
9
8
10
12
原材料t（袋）
28
23
20
25
29
（Ⅰ）请根据所给五组数据，求出t关于x的线性回归方程 $\hat{t} = \hat{b} x + \hat{a}$ ；
（Ⅱ）已知购买原材料的费用C（元）与数量t（袋）的关系为 $C = {\begin{matrix} 300 t + 20 ， (0 < t < 35 ， t \in N) \\ 290 t ， (t \geq 35 ， t \in N) \end{matrix}$ 投入使用的每袋原材料相应的销售收入为600元，多余的原材料只能无偿返还．若餐厅原材料现恰好用完，据悉本次交易会大约有14万人参加，根据（Ⅰ）中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？（注：利润L=销售收入﹣原材料费用）．
（参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ = $\frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ）

查看试题解析
19. 如图，三棱柱ABC﹣A₁B₁C₁中，侧棱AA₁⊥底面ABC， $A B = A C = \frac{1}{2} A A_{1}$ ，AB⊥AC，D是棱BB₁的中点．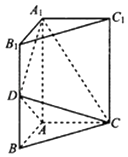
（Ⅰ）证明：平面A₁DC⊥平面ADC；
（Ⅱ）求平面A₁DC与平面ABC所成二面角的余弦值．

查看试题解析
20.
已知直线l的方程为y=x+2，点P是抛物线y²=4x上到直线l距离最小的点，点A是抛物线上异于点P的点，直线AP与直线l交于点Q，过点Q与x轴平行的直线与抛物线y²=4x交于点B．

（Ⅰ）求点P的坐标；
（Ⅱ）证明直线AB恒过定点，并求这个定点的坐标．

查看试题解析
21. 已知函数f（x）=alnx+b（a，b∈R），曲线f（x）在x=1处的切线方程为x﹣y﹣1=0．
（Ⅰ）求a，b的值；
（Ⅱ）证明： $f (x) + \frac{1}{x} \geq 1$ ；
（Ⅲ）已知满足xlnx=1的常数为k．令函数g（x）=me^x+f（x）（其中e是自然对数的底数，e=2.71828…），若x=x₀是g（x）的极值点，且g（x）≤0恒成立，求实数m的取值范围．

查看试题解析
22. 已知α∈[0，π），在直角坐标系xOy中，直线l₁的参数方程为 ${\begin{matrix} x = t c o s α \\ y = t s i n α \end{matrix}$ （t为参数）；在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，直线l₂的极坐标方程是ρcos（θ﹣α）=2sin（α+ $\frac{π}{6}$ ）．
（Ⅰ）求证：l₁⊥l₂
（Ⅱ）设点A的极坐标为（2， $\frac{π}{3}$ ），P为直线l₁ ， l₂的交点，求|OP|•|AP|的最大值．

查看试题解析
23. 已知函数 $f (x) = | x + \sqrt{3 + a}$ |﹣ $| x - \sqrt{1 - a}$ |，其中﹣3≤a≤1．

（Ⅰ）当a=1时，解不等式f（x）≥1；
（Ⅱ）对于任意α∈[﹣3，1]，不等式f（x）≥m的解集为空集，求实数m的取值范围．

查看试题解析

	第一次	第二次	第三次	第四次	第五次
参会人数x（万人）	11	9	8	10	12
原材料t（袋）	28	23	20	25	29