2017年陕西省榆林市高考数学三模试卷（理科）

试卷更新日期：2017-08-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 若复数m（m﹣2）+（m²﹣3m+2）i是纯虚数，则实数m的值为（）

A、0或2 B、2 C、0 D、1或2

查看试题解析
2. 若集合A={x|y= $\sqrt{l g (1 - x)}$ }，B={x|x≥﹣1}，则A∩B等于（）

A、[﹣1，0] B、[﹣1，1） C、（﹣1，+∞） D、（0，1]

查看试题解析
3. 用数学归纳法证明1+2+3+…+n²= $\frac{n^{4} + n^{2}}{2}$ ，则当n=k+1时左端应在n=k的基础上加上（）

A、k²+1 B、（k+1）² C、 $\frac{{(k + 1)}^{4} + {(k + 1)}^{2}}{2}$ D、（k²+1）+（k²+2）+（k²+3）+…+（k+1）²

查看试题解析
4. 函数y=sinx（3sinx+4cosx）（x∈R）的最大值为M，最小正周期为T，则有序数对（M，T）为（）

A、（5，π） B、（4，π） C、（﹣1，2π） D、（4，2π）

查看试题解析
5. 已知数列{a_n}满足a₁=15，且3a_n₊₁=3a_n﹣2，若a_k•a_k₊₁＜0，则正整数k=（）

A、21 B、22 C、23 D、24

查看试题解析
6. 函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜ $\frac{π}{2}$ ）的部分图象如图所示，则ω，φ的值分别为（）

A、2，0 B、2， $\frac{π}{4}$ C、2，﹣ $\frac{π}{3}$ D、2， $\frac{π}{6}$

查看试题解析
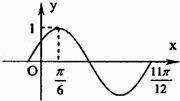7. | $\vec{O A}$ |=1，| $\vec{O B}$ |= $\sqrt{3}$ ， $\vec{O A}$ • $\vec{O B}$ =0，点C在∠AOB内，且∠AOC=30°，设 $\vec{O C}$ =m $\vec{O A}$ +n $\vec{O B}$ （m、n∈R），则 $\frac{m}{n}$ 等于（）

A、 $\frac{1}{3}$ B、3 C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
8. 一个频率分布表（样本容量为30）不小心被损坏了一部分，只记得样本中数据在[20，60）上的频率为0.8，则估计样本在[40，50），[50，60）内的数据个数共为（）

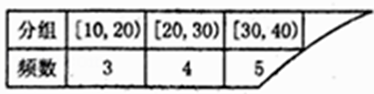A、14 B、15 C、16 D、17

查看试题解析
9. 将一张边长为12cm的正方形纸片按如图（1）所示阴影部分裁去四个全等的等腰三角形，将余下部分沿虚线折叠并拼成一个有底的正四棱锥模型，如图（2）所示放置．如果正四棱锥的主视图是等边三角形，如图（3）所示，则正四棱锥的体积是（）

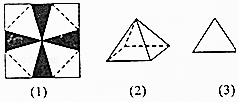A、 $\frac{32}{3} \sqrt{6}$ cm³ B、 $\frac{64}{3} \sqrt{6}$ cm³ C、 $\frac{32}{3} \sqrt{2}$ cm³ D、 $\frac{64}{3} \sqrt{2}$ cm³

查看试题解析
10. 若双曲线 $\frac{x^{2}}{a^{2}} - y^{2} = 1 (a > 0)$ 的一条渐近线与圆x²+（y﹣2）²=2至多有一个交点，则双曲线离心率的取值范围是（）

A、 $[\sqrt{2} ， + \infty)$ B、[2，+∞） C、 $(1 ， \sqrt{2}]$ D、（1，2]

查看试题解析
11. 已知f（x）是定义在R上的奇函数，满足f（﹣ $\frac{3}{2}$ +x）=f（ $\frac{3}{2}$ +x），当x∈[0， $\frac{3}{2}$ ]时，f（x）=ln（x²﹣x+1），则函数f（x）在区间[0，6]上的零点个数是（）

A、3 B、5 C、7 D、9

查看试题解析
12. 秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入x的值为2，则输出的v值为（）

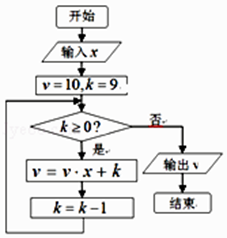A、9×2¹⁰﹣2 B、9×2¹⁰+2 C、9×2¹¹+2 D、9×2¹¹﹣2

查看试题解析

二、填空题

13. 点P（x₀ ， y₀）是曲线y=3lnx+x+k（k∈R）图象上一个定点，过点P的切线方程为4x﹣y﹣1=0，则实数k的值为．

查看试题解析
14. 二项式（ $\sqrt{x}$ ﹣ $\frac{1}{2 x}$ ）ⁿ的展开式中所有项的二项式系数之和是64，则展开式中的常数项为．

查看试题解析
15. 设第一象限内的点（x，y）满足约束条件 ${\begin{matrix} 2 x - y - 6 \leq 0 \\ x - y + 2 \geq 0 \end{matrix}$ ，若目标函数z=ax+by（a＞0，b＞0）的最大值为40，则 $\frac{5}{a} + \frac{1}{b}$ 的最小值为：．

查看试题解析
16. 已知关于空间两条不同直线m，n，两个不同平面α，β，有下列四个命题：①若m∥α且n∥α，则m∥n；②若m⊥β且m⊥n，则n∥β；③若m⊥α且m∥β，则α⊥β；④若n⊂α且m不垂直于α，则m不垂直于n．其中正确命题的序号为．

查看试题解析

三、解答题

17. 在△ABC中，a，b，c分别是角A，B，C的对边，且（a+b+c）（a+b﹣c）=3ab．
（Ⅰ）求角C的值；
（Ⅱ）若c=2，且△ABC为锐角三角形，求a+b的取值范围．

查看试题解析
18. 如图，在三棱锥P﹣ABC中，AC=BC=2，∠ACB=90°，侧面PAB为等边三角形，侧棱 $P C = 2 \sqrt{2}$ ．
（Ⅰ）求证：PC⊥AB；
（Ⅱ）求证：平面PAB⊥平面ABC；
（Ⅲ）求二面角B﹣AP﹣C的余弦值．

查看试题解析
19. 近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重．大气污染可引起心悸、呼吸困难等心肺疾病．为了解某市心肺疾病是否与性别有关，在某医院随机的对入院50人进行了问卷调查得到了如下的列联表：
患心肺疾病
不患心肺疾病
合计
男
5
女
10
合计
50
已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为 $\frac{3}{5}$ ．
（Ⅰ）请将上面的列联表补充完整；
（Ⅱ）是否有99.5%的把握认为患心肺疾病与性别有关？说明你的理由；
（Ⅲ）已知在患心肺疾病的10位女性中，有3位又患胃病．现在从患心肺疾病的10位女性中，选出3名进行其他方面的排查，记选出患胃病的女性人数为ξ，求ξ的分布列，数学期望以及方差；大气污染会引起各种疾病，试浅谈日常生活中如何减少大气污染．
下面的临界值表供参考：
P（K²≥k）
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
（参考公式K²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ 其中n=a+b+c+d）

查看试题解析
20. 已知椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的右焦点为F₂（3，0），离心率为e．
（Ⅰ）若 $e = \frac{\sqrt{3}}{2}$ ，求椭圆的方程；
（Ⅱ）设直线y=kx与椭圆相交于A，B两点，M，N分别为线段AF₂ ， BF₂的中点．若坐标原点O在以MN为直径的圆上，且 $\frac{\sqrt{2}}{2} < e \leq \frac{\sqrt{3}}{2}$ ，求k的取值范围．

查看试题解析
21. 已知函数f（x）=e^x﹣x²+2a+b（x∈R）的图象在x=0处的切线为y=bx．（e为自然对数的底数）．
（Ⅰ）求a，b的值；
（Ⅱ）若k∈Z，且f（x）+ $\frac{1}{2}$ （3x²﹣5x﹣2k）≥0对任意x∈R恒成立，求k的最大值．

查看试题解析
22. 已知直线l的参数方程为 ${\begin{matrix} x = t c o s α \\ y = 1 + t s i n α \end{matrix}$ （0≤α＜π，t为参数），曲线C的极坐标方程为ρ= $\frac{4 c o s θ}{s i n^{2} θ}$ ．
（Ⅰ）将曲线C的极坐标方程化为直角坐标方程，并说明曲线C的形状；
（Ⅱ）若直线l经过点（1，0），求直线l被曲线C截得的线段AB的长．

查看试题解析
23. 已知函数f（x）=log₂（|x+1|+|x﹣2|﹣m）．

(1)、当m=7时，求函数f（x）的定义域；

(2)、若关于x的不等式f（x）≥2的解集是R，求m的取值范围．

查看试题解析

P（K²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

	患心肺疾病	不患心肺疾病	合计
男		5
女	10
合计			50