2017年山东省青岛市高考数学二模试卷（理科）

试卷更新日期：2017-08-12 类型：高考模拟

进入出卷网下载

一、选择题

1. 设全集U=R，集合A={y|y=3﹣x²}，B={x|y=log₂（x+2）}，则（∁_UA）∩B=（）

A、{x|﹣2＜x≤3} B、{x|x＞3} C、{x|x≥3} D、{x|x＜﹣2}

查看试题解析
2. 设复数z=﹣2+i（i为虚数单位），则复数 $z + \frac{1}{z}$ 的虚部为（）

A、 $\frac{4}{5}$ B、 $\frac{4}{5} i$ C、 $\frac{6}{5}$ D、 $\frac{6}{5} i$

查看试题解析
3. 已知命题p，q，“￢p为假”是“p∨q为真”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 一个公司有8名员工，其中6名员工的月工资分别为5200，5300，5500，6100，6500，6600，另两名员工数据不清楚，那么8位员工月工资的中位数不可能是（）

A、5800 B、6000 C、6200 D、6400

查看试题解析
5. 执行如图所示的程序框图，则输出的结果为（）

A、7 B、9 C、10 D、11

查看试题解析
6. 已知x=﹣3，x=1是函数f（x）=sin（ωx+φ）（ω＞0）的两个相邻的极值点，且f（x）在x=﹣1处的导数f'（﹣1）＞0，则f（0）=（）

A、0 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
7. 已知实数m＞1，实数x，y满足不等式组 ${\begin{matrix} y \geq x \\ y \leq 2 x \\ x + y \leq 1 \end{matrix}$ ，若目标函数z=x+my的最大值等于3，则m的值是（）

A、2 B、3 C、4 D、5

查看试题解析
8. 《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高二丈，问：积几何？”其意思为：“今有底面为矩形的屋脊状的锲体，下底面宽3丈，长4丈，上棱长2丈，高2丈，问：它的体积是多少？”已知1丈为10尺，该锲体的三视图如图所示，则该锲体的体积为（）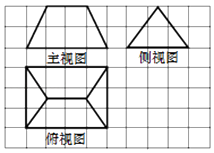

A、10000立方尺 B、11000立方尺 C、12000立方尺 D、13000立方尺

查看试题解析
9. 学校计划利用周五下午第一、二、三节课举办语文、数学、英语、理综4科的专题讲座，每科一节课，每节至少有一科，且数学、理综不安排在同一节，则不同的安排方法共有（）

A、6种 B、24种 C、30种 D、36种

查看试题解析
10. 设F为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）的右焦点，O为坐标原点，若OF的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为 $\frac{2}{3}$ |OF|，则双曲线的离心率为（）

A、 $2 \sqrt{3}$ B、 $\frac{3 \sqrt{5}}{5}$ C、 $2 \sqrt{5}$ D、5

查看试题解析

二、填空题

11. 不等式|2x+1|﹣|5﹣x|＞0的解集为．

查看试题解析
12. 已知向量 $\vec{a}$ ， $\vec{b}$ 的夹角为120°， $\vec{a} = (1 ， \sqrt{3})$ ， $| \vec{a} + \vec{b} | = \sqrt{3}$ ，则 $| \vec{b} |$ = ．

查看试题解析
13. 曲线y=2sinx（0≤x≤π）与直线y=1围成的封闭图形的面积为．

查看试题解析
14. 已知抛物线y²=2x和圆x²+y²﹣x=0，倾斜角为 $\frac{π}{4}$ 的直线l经过抛物线的焦点，若直线l与抛物线和圆的交点自上而下依次为A，B，C，D，则|AB|+|CD|= ．

查看试题解析
15. 若函数f（x）对定义域内的任意x₁ ， x₂ ，当f（x₁）=f（x₂）时，总有x₁=x₂ ，则称函数f（x）为单纯函数，例如函数f（x）=x是单纯函数，但函数f（x）=x²不是单纯函数．若函数 $f (x) = {\begin{matrix} 2^{x} ， x \leq 0 \\ - x^{2} + m ， x > 0 \end{matrix}$ 为单纯函数，则实数m的取值范围是．

查看试题解析

三、解答题

16. 已知函数f（x）= $\frac{\sqrt{3}}{2}$ sin（2x+ $\frac{π}{3}$ ）﹣cos²x+ $\frac{1}{2}$ ．
（Ⅰ）求函数f（x）在[0，π]上的单调递增区间；
（Ⅱ）在△ABC中，a、b、c分别为角A、B、C的对边，f（A）= $\frac{1}{4}$ ，a=3，求△ABC面积的最大值．

查看试题解析
17. 某科技公司生产一种手机加密芯片，其质量按测试指标划分为：指标大于或等于70为合格品，小于70为次品．现随机抽取这种芯片共120件进行检测，检测结果统计如表：
测试指标
[50，60）
[60，70）
[70，80）
[80，90）
[90，100]
芯片数量（件）
8
22
45
37
8
已知生产一件芯片，若是合格品可盈利400元，若是次品则亏损50元．
（Ⅰ）试估计生产一件芯片为合格品的概率；并求生产3件芯片所获得的利润不少于700元的概率．
（Ⅱ）记ξ为生产4件芯片所得的总利润，求随机变量ξ的分布列和数学期望．

查看试题解析
18.
在三棱柱ABC﹣A₁B₁C₁中，侧面ABB₁A₁为矩形，AB=2，AA₁=2 $\sqrt{2}$ ，D是AA₁的中点，BD与AB₁交于点O，且CO⊥平面ABB₁A₁ ．

（Ⅰ）证明：平面AB₁C⊥平面BCD；
（Ⅱ）若OC=OA，△AB₁C的重心为G，求直线GD与平面ABC所成角的正弦值．

查看试题解析
19. 在公差不为0的等差数列{a_n}中，a₂²=a₃+a₆ ，且a₃为a₁与a₁₁的等比中项．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）设b_n=（﹣1）ⁿ $\frac{n}{(a_{n} - \frac{1}{2}) (a_{n + 1} - \frac{1}{2})}$ ，求数列{b_n}的前n项和T_n ．

查看试题解析
20. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}}$ =1（a＞b＞0）的左、右顶点分别为A₁、A₂ ，上、下顶点分别为B₂、B₁ ， O为坐标原点，四边形A₁B₁A₂B₂的面积为4，且该四边形内切圆的方程为x²+y²= $\frac{4}{5}$ ．

（Ⅰ）求椭圆C的方程；
（Ⅱ）若M、N是椭圆C上的两个不同的动点，直线OM、ON的斜率之积等于﹣ $\frac{1}{4}$ ，试探求△OMN的面积是否为定值，并说明理由．

查看试题解析
21. 已知函数f（x）=（1﹣m）lnx+ $\frac{m}{2} x^{2}$ ﹣x，m∈R且m≠0．
（Ⅰ）当m=2时，令g（x）=f（x）+log₂（3k﹣1），k为常数，求函数y=g（x）的零点的个数；
（Ⅱ）若不等式f（x）＞1﹣ $\frac{1}{m}$ 在x∈[1，+∞）上恒成立，求实数m的取值范围．

查看试题解析

测试指标	[50，60）	[60，70）	[70，80）	[80，90）	[90，100]
芯片数量（件）	8	22	45	37	8