2017年山东省聊城市高考数学三模试卷(理科)
试卷更新日期:2017-08-12 类型:高考模拟
一、选择题
-
1. 设i是虚数单位,若 = ,则复数z的虚部为( )A、﹣2 B、2 C、﹣1 D、12. 已知集合A={x|x2+x﹣6>0},集合B={x|﹣1<x<3},若a∈(A∪B),则a可以是( )A、﹣3 B、﹣2 C、﹣1 D、33. 要得到函数 图象,只需将函数 图象( )A、向左平移 个单位 B、向右平移 个单位 C、向左平移 个单位 D、向右平移 个单位4. 某单位招聘员工,有200名应聘者参加笔试,随机抽查了其中20名应聘者笔试试卷,统计他们的成绩如下表:
分数段
[60,65)
[65,70)
[70,75)
[75,80)
[80,85)
[85,90)
[90,95)
人数
1
3
6
6
2
1
1
若按笔试成绩择优录取40名参加面试,由此可预测参加面试的分数线为( )
A、70分 B、75分 C、80分 D、85分5. 已知函数f(x)在R上单调递增,若∃x∈R,f(|x+1|)≤f(log2a﹣|x+2|),则实数a的取值范围是( )A、[2,+∞) B、[4,+∞) C、[8,+∞) D、(0,2]6. 已知一个几何体的三视图如图所示,则该几何体的体积为( )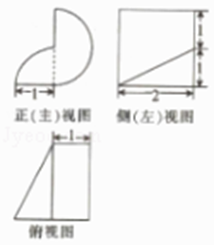 A、2π B、 C、 D、7. “m≤”是“函数f(x)=2 的值不小于4”的( )
A、2π B、 C、 D、7. “m≤”是“函数f(x)=2 的值不小于4”的( )
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件8. 已知两点A(﹣m,0)和B(2+m,0)(m>0),若在直线l:x+ y﹣9=0上存在点P,使得PA⊥PB,则实数m的取值范围是( )A、(0,3) B、(0,4) C、[3,+∞) D、[4,+∞)9. 已知变量x、y满足约束条件 ,且z=x+2y的最小值为3,则 ≥ 的概率是( )A、 B、 C、 D、10. 若函数f(x)=alog2(|x|+4)+x2+a2﹣8有唯一的零点,则实数a的值是( )A、﹣4 B、2 C、±2 D、﹣4或2二、填空题
-
11. (x2﹣ )5的展开式中常数项为 .12. 如图是一个程序框图,则输出的S的值是
 13. 已知非零向量 、 满足| ﹣ |=| +2 |,且 与 的夹角的余弦值为﹣ ,则 = .14. 已知双曲线C: ﹣ =1(a>0,b>0)的左顶点为A,点B(0, b),若线段AB的垂直平分线过右焦点F,则双曲线C的离心率为 .15. 若函数f(x)=(x2﹣ax+a+1)ex(a∈N)在区间(1,3)只有1个极值点,则曲线f(x)在点(0,f(0))处切线的方程为 .
13. 已知非零向量 、 满足| ﹣ |=| +2 |,且 与 的夹角的余弦值为﹣ ,则 = .14. 已知双曲线C: ﹣ =1(a>0,b>0)的左顶点为A,点B(0, b),若线段AB的垂直平分线过右焦点F,则双曲线C的离心率为 .15. 若函数f(x)=(x2﹣ax+a+1)ex(a∈N)在区间(1,3)只有1个极值点,则曲线f(x)在点(0,f(0))处切线的方程为 .三、解答题
-
16. 已知函数f(x)=sin(2x+φ)+2sin2x(|φ|< )的图象过点( , ).(1)、求函数f(x)在[0, ]的最小值;(2)、设角C为锐角,△ABC的内角A、B、C的对边长分别为a、b、c,若x=C是曲线y=f(x)的一条对称轴,且△ABC的面积为2 ,a+b=6,求边c的长.17. 如图,在直三棱柱ABC﹣A1B1C1中,D是A1B1的中点.
 (1)、求证:A1C∥平面BDC1;(2)、若AB⊥AC,且AB=AC= AA1 , 求二面角A﹣BD﹣C1的余弦值.18. 已知等差数列{an}的前n项和为Sn , a1=a,当n≥2时, =3n2an+S ,an≠0,n∈N*.(1)、求a的值;(2)、设数列{cn}的前n项和为Tn , 且cn=3n﹣1+a5 , 求使不等式4Tn>S10成立的最小正整数n的值.19. 某地区拟建立一个艺术搏物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标总是中随机抽取3个总题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正面回答每道题目的概率均为 ,甲、乙两家公司对每题的回答都是相独立,互不影响的.(1)、求甲、乙两家公司共答对2道题目的概率;(2)、请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?20. 已知函数f(x)=x2+ax﹣lnx(a∈R,a为常数)(1)、当a=﹣1时,若方程f(x)= 有实根,求b的最小值;(2)、设F(x)=f(x)•e﹣x , 若F(x)在区间(0,1]上是单调函数,求a的取值范围.21. 已知右焦点为F的椭圆C: + =1(a>b>0)过点M(1, ),直线x=a与抛物线L:x2= y交于点N,且 = ,其中O为坐标原点.(1)、求椭圆C的方程;(2)、直线l与椭圆C交于A、B两点.
(1)、求证:A1C∥平面BDC1;(2)、若AB⊥AC,且AB=AC= AA1 , 求二面角A﹣BD﹣C1的余弦值.18. 已知等差数列{an}的前n项和为Sn , a1=a,当n≥2时, =3n2an+S ,an≠0,n∈N*.(1)、求a的值;(2)、设数列{cn}的前n项和为Tn , 且cn=3n﹣1+a5 , 求使不等式4Tn>S10成立的最小正整数n的值.19. 某地区拟建立一个艺术搏物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标总是中随机抽取3个总题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正面回答每道题目的概率均为 ,甲、乙两家公司对每题的回答都是相独立,互不影响的.(1)、求甲、乙两家公司共答对2道题目的概率;(2)、请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?20. 已知函数f(x)=x2+ax﹣lnx(a∈R,a为常数)(1)、当a=﹣1时,若方程f(x)= 有实根,求b的最小值;(2)、设F(x)=f(x)•e﹣x , 若F(x)在区间(0,1]上是单调函数,求a的取值范围.21. 已知右焦点为F的椭圆C: + =1(a>b>0)过点M(1, ),直线x=a与抛物线L:x2= y交于点N,且 = ,其中O为坐标原点.(1)、求椭圆C的方程;(2)、直线l与椭圆C交于A、B两点.①若直线l与x轴垂直,过点P(4,0)的直线PB交椭圆C于另一点E,证明直线AE与x轴相交于定点;
②已知D为椭圆C的左顶点,若l与直线DM平行,判断直线MA,MB是否关于直线FM对称,并说明理由.