初中数学苏科版七年级下册7.5 多边形的内角和与外角和 同步练习
试卷更新日期：2020-02-10 类型：同步测试
一、选择题（每题3分，计18分）
-
1. 在△ABC中，∠A=20°，∠B=60°，则△ABC的形状是（ ）A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形2. 将一个n边形变成n+1边形，内角和将（ ）A、减少180° B、增加90° C、增加180° D、增加360°3. 如图，在四边形ABCD 中，∠A+∠D=α，∠ABC 的平分线与∠BCD 的平分线交于点 P，则∠P=（ ）
A、90°﹣ α B、90°+ α C、 α D、360°﹣ α4. 如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为（ ）
A、13 B、14 C、15 D、165. 一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是（ ）A、27 B、35 C、44 D、546. 在四边形ABCD中，∠A＝∠B＝∠C，点E在边AB上，∠AED＝60°，则一定有（ ）A、∠ADE＝20° B、∠ADE＝30° C、∠ADE＝ ∠ADC D、∠ADE＝ ∠ADC二、填空题（每题3分，计24分）
-
7. 如图，是一副三角板叠放的示意图，则∠α= ．
8. 在△ABC中，∠A=100°，∠B=3∠C，则∠B=度．9. 如图，∠1+∠2+∠3+∠4=度．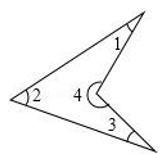
10. 如图，平面镜 A 与 B 之间夹角为 120°，光线经过平面镜 A 反射后射在平面镜 B 上，再反射出去，若∠1=∠2，则∠1=度．
11. 在 Rt△ABC 中，锐角 A 的平分线与锐角 B 的邻补角的平分线相交于点 D，则∠ADB=度．12. 如图，△ABC 中，∠B=∠C，FD⊥BC 于 D，DE⊥AB 于 E，∠AFD=158°， 则∠EDF 等于度．
13. 已知：如图，直线 AB、CD 相交于点 O，PE⊥AB 于点 E，PF⊥CD 于点 F，如果∠AOC=50°，那么∠EPF=度．
14. 小明在阅览时发现这样一个问题“在某次聚会中，共有 6 人参加，如果每两人都握一次手，共握几次手？”，小明通过努力得出了答案．为了解决更一般的问题，小明设计了下列图表进行探究：请你在图表右下角的横线上填上你归纳出的一般结论（填入最后一个图下的空线上）．参加人数
2
3
4
5
…
n
握手示意图
握手次数
1
2+1=3
3+2+1=6
4+3+2+1=10
…
三、解答题（前6题每题8分，最后1题10份，计58分）
-
15. 如图，在直角△ABC 中，∠ACB=90°，CD 是高，∠1=35°，求∠2，∠B 与∠A 的度数．
16. 如图，若∠B=40°，∠C=71°，∠BME=133°，∠EPB=140°，∠F=47°．求∠A，∠D．
17. 如图，已知三角形 ABC 的三个内角平分线交于点 I，IH⊥BC 于 H，试比较∠CIH 和∠BID 的大小．
18. 如图，已知∠1=∠2，∠3=∠4．
(1)、若∠A=100°，求x的值；(2)、若∠A=n°，求x的值．19. 在△ABC 中，∠A= （∠B+∠C）、∠B﹣∠C=20°，求∠A、∠B、∠C 的度数．20. 如图
(1)、如图①，△ABC 是锐角三角形，高 BD、CE 相交于点 H，找出∠BHC和∠A 之间存在何种等量关系；
(2)、如图②，若△ABC 是钝角三角形，∠A＞90°，高 BD、CE 所在的直线相交于点 H，把图②补充完整，并指出此时（1）中的等量关系是否仍然成立？21. 如图
(1)、如图①所示，∠1+∠2 与∠B+∠C 有什么关系？为什么？(2)、如图②若把△ABC 纸片沿 DE 点折叠当点 A 落在四边形 BCED 内部时， 则∠A 与∠α+∠β之间有一种数量关系始终保持不变，请写出这个规律并说明理由．四、选择题:(每题3分，计6分)
-
22. 如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（ ）
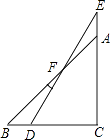A、15° B、25° C、30° D、10°23. 如图是一枚“八一”建军节纪念章，其外轮廓是一个正五边形， 则图中∠1 的大小为（ ）．
A、120° B、36° C、108° D、90°五、填空题:(每题3分，计6分)
-
24. 如图，∠ACD 是△ABC 的外角，∠ABC 的平分线与∠ACD 的平分线交于点A1 ， ∠A1BC 的平分线与∠A1CD 的平分线交于点 A2 ， …，∠An﹣1BC 的平分线与∠An﹣1CD 的平分线交于点 An ． 设∠A=θ．则：
(1)、∠A1=；(2)、∠An= ．25. 一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M.如果∠ADF=100°，那么∠BMD为度.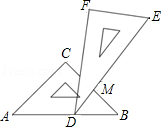
六、解答题:(第5题8分，第6题10分，第5题10分)
-
26. △ABC 中，三个内角的度数均为整数，且∠A＜∠B＜∠C，4∠C=7∠A，求∠A 的度数．
27. 如图，
△ABC 中，分别延长△ABC 的边 AB、AC 到 D、E，∠CBD 与∠BCE的平分线相交于点 P，爱动脑筋的小明在写作业的时发现
如下规律：
(1)、若∠A=50°，则∠P=°；(2)、若∠A=90°，则∠P=°；(3)、若∠A=100°，则∠P=°；(4)、请你用数学表达式归纳∠A 与∠P 的关系，并说明理由．28. Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．
(1)、若点 P 在线段 AB 上，如图（1）所示，且∠α=50°，则∠1+∠2=°；(2)、若点 P 在边 AB 上运动，如图（2）所示，则∠α、∠1、∠2 之间的关系为：；(3)、若点P运动到边 AB 的延长线上，如图（3）所示，则∠α、∠1、∠2 之间有何关系？猜想并说明理由．(4)、若点P运动到△ABC 形外，如图（4）所示，则∠α、∠1、∠2 之间的关系为： ．