初中数学苏科版七年级下册11.4-11.5 解一元一次不等式 用不等式解决问题 同步练习
试卷更新日期：2020-02-10 类型：同步测试
一、选择题（每题3分，共18分）
-
1. 下列不等式中，是一元一次不等式的是（ ）A、x+1＞2 B、 ＞9 C、2x+y≤5 D、2. 不等式-3x+6≥9 的解集在数轴上表示正确的是（ ）A、
B、
C、
D、
3. 小华拿27元钱购买圆珠笔和练习册，已知一本练习册2元，已知圆珠笔1元，他买了4本练习册，x支圆珠笔，则关于x的不等式表示正确的是（ ）A、2×4+x＜27 B、2×4+x≤27 C、2x+4≤27 D、2x+4≥274. 不等式 6-4x≥3x-8 的正整数解为（ ）A、2 个 B、3 个 C、4 个 D、5 个5. 若关于 x 的一元一次方程 x-m+2=0 的解是负数，则 m 的取值范围是（ ）A、m≥2 B、m＞2 C、m＜2 D、m≤26. 某乒乓球馆有两种计费方案，如下图表．李强和同学们打算周末去此乒乓球馆连续打球 4 小时，经服务生测算后，告知他们包场计费方案会比人数计费方案便宜，则他们参与包场的人数至少为（ ）
A、9 B、8 C、7 D、6二、填空题（每题4分，共32分）
-
7. 不等式 6x+8＞3x+17 的解集是.8. 当 x时，代数式 14-2x 的值是非负数．9. 当 a=时，关于 x 的不等式 2x-a＞-3 的解集如图．
10. 某次知识竞赛共20道题，每一题答对得10分，答错或不答都扣5分，小明得分要超过160 分．设他答对了 x 道题，则根据题意可列不等式.11. 不等式 3x-2≥4（x-1）的所有非负整数解的和为.12. 一块长方形的菜地，长比宽多 3m，周长不超过 30m．那么这块菜地的长最多是m．13.对一个实数x按如图所示的程序进行操作，规定：程序运行从“输入一个实数x”到“结果是否大于88？”为一次操作．如果操作只进行一次就停止，则x的取值范围是 ．
14. 出租车按分段累加的方法收费：3公里以内（含3公里）收5元；超过3公里且不超过10公里的部分每公里收2元；超过10公里的部分每公里收3元．每次坐车另加燃油附加费1元，不足1公里以1公里计算．若小明从学校坐出租车到家用了38元的钱，设小明家到学校的距离为x公里，则x的取值范围是.三、解答题（50分）
-
15. 解不等式 ，并将解集在数轴上表示出来.
16.小明解不等式 的过程如图．请指出他解答过程中错误步骤的序号，并写出正确的解答过程．
17. 已知不等式 7-2x＞3 的正整数解是方程 3x-a=2ax-6 的解，求（3-4a）（3+4a）+（3+4a）2的值．18. 对于任意实数 a，b，定义关于“⊗ ”的一种运算如下：a⊗ b=2a-b．例如 ：5⊗ 2=2×5-2=8，（-3）⊗ 4=2×（-3）-4=-10．(1)、若 3⊗ x=-2011，求x的值；(2)、若 x⊗ 3＜5，求x的取值范围．19. 关于x的两个不等式① 与②1-3x＞0．(1)、若两个不等式的解集相同，求a的值．(2)、若不等式①的解都是②的解，求a的取值范围．20. 某机器人公司为扩大经营，决定购进 6 台机器用于生产某种小机器人．现有甲、乙两种机器供选择，其中每台机器的价格和日生产量如下表所示．经过预算，本次购买机器的费用不能超过 34 万元．甲种机器
乙种机器
价格/（万元/台）
5
7
每台机器的日生产量/个
60
100
(1)、按要求该公司有几种购买方案？(2)、若该公司购进的6台机器的日生产量不能少于380个，那么为了节约资金，应选择哪种购买方案？四、选择题（每题5分，共10分）
-
21. 若关于x的不等式mx-n＞0 的解集为 ，则关于x的不等式（m+n）x＞m-n 的解集为（ ）A、 B、 C、 D、22. 运行程序如图所示，从“输入实数 x”到“结果是否＜18”为一次程序操作，若输入 x 后程序操作仅进行了三次就停止，那么 x 的取值范围是（ ）
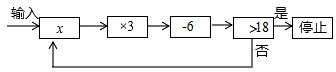A、 B、 C、 D、五、填空题（每题5分，共10分）