初中数学苏科版七年级下册9.5 多项式的因式分解 同步练习

试卷更新日期：2020-02-10 类型：同步测试

进入 出卷网 下载

一、选择题（每小题3分，共18分）

  • 1. 多项式 2x2-4xy+2x 提取公因式 2x 后，另一个因式为（   ）
    A、x-2y B、x-2y+1 C、x-4y+1 D、x-2y-1

    查看试题解析

  • 2. 下列分解因式正确的是（   ）
    A、-ma-m=-m（a-1） B、a2-1=（a-1）2 C、a2-6a+9=（a-3）2 D、a2+3a+9=（a+3）2

    查看试题解析

  • 3. 下列各式从左到右的变形中，为因式分解的是（   ）
    A、x（a-b）=ax-bx B、x2-1+y2=（x-1）（x+1）+y2 C、y2-1=（y+1）（y-1） D、ax+by+c=x（a+b）+c

    查看试题解析

  • 4. 分解因式a2b-b3结果正确的是（ ）
    A、b(a+b)(a-b) B、b(a-b)2 C、b(a2-b2) D、b(a+b)2

    查看试题解析

  • 5. 若 4×2-2（k-1）x+9 是完全平方式，则 k 的值为（   ）
    A、±5 B、5 或-7 C、-5 或 7 D、±7

    查看试题解析

  • 6. 已知 a-b=1，a2+b2=25，则 a+b 的值为（   ）
    A、7 B、-7 C、±9 D、±7

    查看试题解析

二、填空题（每小题3分，共24分）

  • 7. 分解因式： x2 －9= ．

    查看试题解析

  • 8. 多项式2a2b3+6ab2的公因式是 ．

    查看试题解析

  • 9. 请你写一个能先提公因式，再运用完全平方公式来分解因式的三次三项式，并写出分解因式的结果 ．

    查看试题解析

  • 10. 若一个长方形的长、宽分别为 a、b，周长为 12，面积为 8，则 a2b+ab2=

    查看试题解析

  • 11. 已知 a2-a-1=0，则 a3-a2-a+2018=

    查看试题解析

  • 12. 观察图形，根据图 1 面积的关系，不需要连其他的线，便可以得到一个一个多项式的因式分解 ．

    图 1

    查看试题解析

  • 13. 若一个正方形的面积为 4a2+12ab+9b2（a＞0，b＞0），则这个正方形的边长为 ．

    查看试题解析

  • 14. 若△ABC 的三边长为 a，b，c，且 c（a-b）+b（b-a）=0，则△ABC 为三角形．

    查看试题解析

三、解答题（58分）

  • 15. 把下列多项式因式分解：
    (1)、ax2-16ay2；
    (2)、a3+ab2-2a2b；
    (3)、x2y（m-n）-xy2（n-m）
    (4)、a2+2ab+b2-9a

    查看试题解析

  • 16. 如图 ，将一块长为 a（cm）的正方形纸片的四角个剪去一个边长为 bcm（b＜ a2 ）的小正方形．用含 a，b 的代数式表示剩余部分的面积，并用分解因式法求当 a=9.7cm， b=0.15cm 时，剩余部分的面积．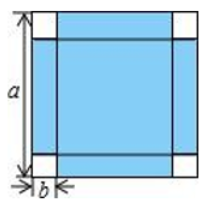


    查看试题解析

  • 17. 如图 ，边长为 a，b 的矩形，它的周长为 14，面积为 10，求下列各式的值：


    (1)、a2b+ab2；
    (2)、a2+b2+ab．

    查看试题解析

  • 18.     
    (1)、因式分解：（x-y）（3x-y）+2x（3x-y）；
    (2)、设 y=kx，是否存在实数 k，使得上式的化简结果为 x2？求出所有满足条件的 k 的值．若不能，请说明理由．

    查看试题解析

  • 19. 已知 a，b，c 为△ABC 的三条边的长．试判断代数式（a2-2ac+c2）-b2 的值的符号，并说明理由．

    查看试题解析

  • 20. 已知 4m+n=40，2m-3n=5．求（m+2n）2-（3m-n）2 的值．

    查看试题解析

  • 21. 阅读材料：若 m2-2mn+2n2-8n+16=0，求 m、n 的值．根据你的观察，探究下面的

    问题：

    (1)、已知 x2+2xy+2y2+2y+1=0，求 2x+y 的值；
    (2)、已知 a-b=4，ab+c2-6c+13=0，求 a+b+c 的值．

    查看试题解析

四、选择题（每小题5分，共10分）

  • 22. 2x3-x2-5x+k 中，有一个因式为（x-2），则 k 值为（   ）
    A、2 B、6 C、-6 D、-2

    查看试题解析

  • 23. 现有一列式子：①552-452；②5552-4452；③55552-44452…则第⑧个式子的计算结果用科学记数法可表示为（   ）
    A、1.1111111×1016 B、1.1111111×1027 C、1.111111×1056 D、1.1111111×1017

    查看试题解析

五、填空题（每小题5分，共10分）

六、解答题（10分）

  • 26. 我们知道：“多项式 a2+2ab+b2 及 a2-2ab+b2 叫做完全平方式”，如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．

    例如：分解因式 x2+2x-3=（x2+2x+1）-4=（x+1）2-4=（x+1+2）（x+1-2）=（x+3）（x-1）；
    例如求代数式 2x2+4x-6 的最小值.
    2x2+4x-6=2（x2+2x-3）=2（x+1）2-8．
    可知当 x=-1 时， 2x2+4x-6 有最小值，最小值是-8，根据阅读材料用配方法解决下列问题：

    (1)、分解因式：m2-4m-5= ．
    (2)、解：当 a，b 为何值时，多项式 a2+b2-4a+6b+18 有最小值，并求出这个最小值．
    (3)、当 a，b 为何值时，多项式 a2-2ab+2b2-2a-4b+27 有最小值，并求出这个最小值．

    查看试题解析