初中数学苏科版八年级下册11.3 反比例函数的应用 同步练习
试卷更新日期:2020-02-10 类型:同步测试
一、选择题(每小题4分,共24分)
-
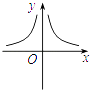
1. 在 中, 是 的( ).A、一次函数 B、反比例函数 C、正比例函数 D、既不是正比例函数,也不是反比例函数2. 若当 时,正比例函数 与反比例函数 的值相等,则 与 的比是( ).A、16:1 B、4:1 C、1:4 D、1:163. 已知反比例函数 的图象如图所示,则实数m的取值范围是( ).
 A、m>2 B、m>0 C、m<2 D、m<04. 如果点P为反比例函数 的图象上的一点,PQ垂直于x轴,垂足为Q,那么 POQ的面积为( ).A、8 B、4 C、2 D、15. 如图,已知三角形的面积一定,则其底边a和该底边上的高h之间的函数关系图象大致是( )
A、m>2 B、m>0 C、m<2 D、m<04. 如果点P为反比例函数 的图象上的一点,PQ垂直于x轴,垂足为Q,那么 POQ的面积为( ).A、8 B、4 C、2 D、15. 如图,已知三角形的面积一定,则其底边a和该底边上的高h之间的函数关系图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 设直线 与双曲线 相交于P,Q两点,0为坐标原点,则∠POQ是( ).A、锐角 B、直角 C、钝角 D、锐角或钝角
6. 设直线 与双曲线 相交于P,Q两点,0为坐标原点,则∠POQ是( ).A、锐角 B、直角 C、钝角 D、锐角或钝角二、填空题(每小题3分,共24分)
-
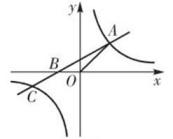
7. 若 与 成反比例关系, 与 成反比例关系,则 与 成关系.8. 已知 与 成反比例,且当 =-2时, =4,则 与 的函数关系式是.9. 已知 与(2 -1)成反比例且当 =0时, =2,那么当 =1时, =.10. 已知点A(1,4- )在双曲线 ,则常数 的值为.11. 如图,过点A(1,0)的直线与 轴平行,且分别与正比例函数 , 和反比例函数 但在第一象限相交,则 的大小关系是.
 12. 已知双曲线 ( 为常数)与直线 交于A点,A点的纵坐标为2,则双曲线关系式为.
12. 已知双曲线 ( 为常数)与直线 交于A点,A点的纵坐标为2,则双曲线关系式为.
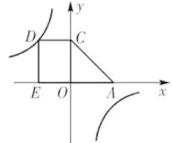
13. 小刚欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为900牛顿和0.5米,则当动力臂为1.5米时,撬动石头需要的力大于牛顿.(提示根据杠杆原理:阻力x阻力臂=动力x动力臂)14. 如图,直线 与 轴、 轴分别相交于点A,B,四边形ABCD是正方形,曲线 在第一象限经过点D,则 =.
三、解答题(共52分)
-
15. 已知 , 与 成反比例, 与 成正比例,且 =3时, =5; =1时, =-1.求 与 之间的函数关系式.16. 如图,D为反比例函数 的图象上一点,过D作DE⊥ 轴于点E,DC⊥ 轴于点C,一次函数 的图象经过C点,与 轴相交于A点,四边形DCAE的面积为4,求 的值.
 17. 已知直线 与双曲线 交于点 .(1)、求 的值;(2)、若点 在双曲线 上,且 ,试比较 , 的大小.18. 某项工程需要砂石料 立方米,阳光公司承担了该工程运送砂石料的任务.(1)、在这项任务中平均每天的工作量V(立方米/天)与完成任务所需的时间 (天)之间具有怎样的函数关系?写出这个函数关系式.(2)、阳光公司计划投入A型卡车200辆,每天一共可以运送砂石料2x104立方米,则完成全部运送任务需多少天?(3)、如果工作了25天后,由于工程进度的需要,公司准备再投人A型卡车120辆,在保证每辆车每天工作量不变的前提下,问是否能提前28天完成任务?
17. 已知直线 与双曲线 交于点 .(1)、求 的值;(2)、若点 在双曲线 上,且 ,试比较 , 的大小.18. 某项工程需要砂石料 立方米,阳光公司承担了该工程运送砂石料的任务.(1)、在这项任务中平均每天的工作量V(立方米/天)与完成任务所需的时间 (天)之间具有怎样的函数关系?写出这个函数关系式.(2)、阳光公司计划投入A型卡车200辆,每天一共可以运送砂石料2x104立方米,则完成全部运送任务需多少天?(3)、如果工作了25天后,由于工程进度的需要,公司准备再投人A型卡车120辆,在保证每辆车每天工作量不变的前提下,问是否能提前28天完成任务?四、能力挑战(满分:30分)