初中数学苏科版八年级下册9.3 平行四边形 同步练习
试卷更新日期：2020-02-10 类型：同步测试
一、选择题
-
1. 在四边形ABCD中，O是对角线交点，下列条件中，不能判定四边形ABCD是平行四边形的是（ ）.A、AD//BC，AD=BC B、AB=DC，AD=BC C、AB//DC，AD=BC D、OA=OC，OD=OB2. 在四边形ABCD中，∠A：∠B：∠C：∠D的比例依次如下，其中能使四边形ABCD是平行四边形的是（ ）A、1：2：3：4 B、2：2：3：3 C、2：3：3：2 D、2：3：2：33. 如果平行四边形两邻边的长分别为3，4，那么其对角线的长可能是（ ）.A、1 B、3 C、7 D、94. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应假设这个三角形中（ ）A、有一个内角大于60° B、有一个内角小于60° C、每一个内角都大于60° D、每一个内角都小于60°5. 平行四边形ABCD中，若AB，BC，CD三条边的长度分别为( -2)cm，( +3)cm，8 cm，则平行四边形ABCD的周长是（ ）.A、46 cm B、36 cm C、31 cm D、42 cm6. 如图，已知 ABCD的两条对角线AC与BD交于平面直角坐标系的原点，点A的坐标为(-2，3)，则点C的坐标为（ ）
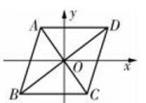A、(-3，2) B、(-2，-3) C、(3，-2) D、(2，-3)二、填空题
-
7. 如果平行四边形的周长为56 cm,两邻边的长度比为3:1，那么这个平行四边形较长边的长为cm.8. 在▱ABCD中，∠B=50°，AB=5cm， BC=7cm，则∠D=°， ABCD的周长为cm.9. 如图，在 ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则线段BE，EC的长度分别为.
10. 在四边形ABCD中，对角线AC,BD相交于点O,若OA=OC,要使四边形ABCD成为平行四边形，则可添加的条件为(填一个即可)11. 平行四边形ABCD中，对角线AC,BD交于点O,AC=6cm ,BD=8cm,则边AB长度 的取值范围是.12. 如图，在 ABCD中，∠ODA =90°，AC=10 cm，BD=6cm，则AD的长为cm.
三、解答题(每题13分,共52分)
-
13. 如图，在 ABCD中，对角线AC，BD交于点O，经过点O的直线交AB于点E，交CD于点F.
求证：OE=OF.
14. 如图，四边形ABCD是平行四边形，DE平分∠ADC交AB于点E，BF平分∠ABC交CD于点F
(1)、求证：DE=BF；(2)、连接EF，写出图中所有的全等三角形.15. 用反证法证明：等腰三角形的底角是锐角．16. 如图，四边形ABCD是平行四边形，E，F是对角线AC上的两点，∠1=∠2.
求证：
(1)、AE=CF；(2)、四边形EBFD是平行四边形.四、选择题(每小题5分,共10分)
-
17. 在四边形ABCD中，现有以下条件：①AB//CD，②A B=CD，③BC//AD，④BC=AD，从中任选两个使四边形ABCD为平行四边形的选法有（ ）.A、3种 B、4种 C、5种 D、6种18. 若以A(－0.5，0)，B(2，0)，C(0，1)三点为顶点画平行四边形，则第四个顶点不可能在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限
五、填空题(每小题5分,共10分)
