人教版数学八年级上册第14章 14.2.1平方差公式 同步练习
试卷更新日期：2017-08-10 类型：同步测试
一、单选题
-
1. 下列运用平方差公式计算，错误的是（ ）A、（a+b）（a﹣b）=a2﹣b2 B、（x+1）（x﹣1）=x2﹣1 C、（2x+1）（2x﹣1）=2x2﹣1 D、（﹣3x+2）（﹣3x﹣2）=9x2﹣42. 如图，根据计算正方形ABCD的面积，可以说明下列哪个等式成立（ ）
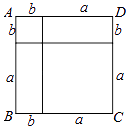A、（a﹣b）2=a2﹣2ab+b2 B、（a+b）2=a2+2ab+b2 C、（a+b）（a﹣b）=a2﹣b2 D、a（a﹣b）=a2﹣ab3. 下列各式中，计算正确的是（ ）A、（15x2y﹣5xy2）÷5xy=3x﹣5y B、98×102=（100﹣2）（100+2）=9996 C、 D、（3x+1）（x﹣2）=3x2+x﹣24. 下列计算正确的是（ ）A、（x+y）2=x2+y2 B、（x﹣y）2=x2﹣2xy﹣y2 C、（x+1）（x﹣1）=x2﹣1 D、（x﹣1）2=x2﹣15. 化简（m2+1）（m+1）（m﹣1）﹣（m4+1）的值是（ ）A、﹣2m2 B、0 C、﹣1 D、﹣26. 下列各式能用平方差公式计算的是（ ）A、（﹣3a﹣b）（﹣3a+b） B、（3a+b）（a﹣b） C、（3a+b）（﹣3a﹣b） D、（﹣3a+b）（3a﹣b）7. 下列变形正确的是（ ）A、（﹣3a3）2=﹣9a5 B、2x2y﹣2xy2=0 C、﹣ ÷2ab=﹣ D、（2x+y）（x﹣2y）=2x2﹣2y28. 计算（a﹣2）（﹣a﹣2）的结果正确的是（ ）A、a2﹣4 B、a2﹣4a+4 C、4﹣a2 D、2﹣a29. 下列计算正确的是（ ）A、（2x﹣3）2=4x2+12x﹣9 B、（4x+1）2=16x2+8x+1 C、（a+b）（a﹣b）=a2+b2 D、（2m+3）（2m﹣3）=4m2﹣310. 如图，从边长为（a+4）cm的正方形纸片中剪去一个边长为（a+1）cm的正方形．（a＞0）剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙）则矩形的面积为（ ）
A、（2a2+5a）cm2 B、（3a+15）cm2 C、（6a+9）cm2 D、（6a+15）cm211.在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（ ）
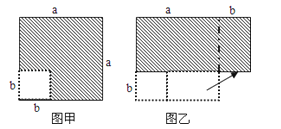A、（a+b）2=a2+2ab+b2 B、（a﹣b）2=a2﹣2ab+b2 C、a2﹣b2=（a+b）（a﹣b） D、（a+2b）（a﹣b）=a2+ab﹣2b2二、填空题
-
12. 计算： = ．13. 若a2﹣b2= ，a﹣b= ，则a+b的值为 ．14.
如图，在边长为a的正方形中剪去一个边长为b的小正方形（a＞b），把剩下的部分拼成一个梯形，分别计算这两个图形阴影部分的面积，验证了公式 ．
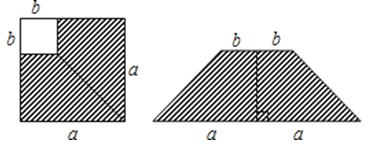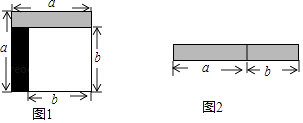
15. 已知：（x﹣2）0无意义，请你计算（2x+1）2﹣（2x+5）（2x﹣5）= ．16. 如图，边长为m+4的正方形纸片剪出一个边长为m的正方形之后，剩余部分可剪拼成一个矩形，若拼成的矩形一边长为4，则另一边长为 ．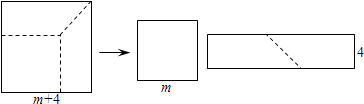
17. 从边长为a的正方形中剪掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2），上述操作过程能验证的等式是 ． （请填入正确答案的序号）①a2﹣2ab+b2=（a﹣b）2；
②a2﹣b2=（a+b）（a﹣b）；
③a2+ab=a（a+b）．
三、解答题