2017年浙江中考真题分类汇编（数学）：专题08 三角形

试卷更新日期：2017-08-10 类型：二轮复习

进入出卷网下载

一、单选题

1. 下列各组数中，不可能成为一个三角形三边长的是（ )

A、2，3，4 B、5，7，7 C、5，6，12 D、6，8，10

查看试题解析
2.
如图，已知△ABC，AB=AC，若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（）

A、AE=EC B、AE=BE C、∠EBC=∠BAC D、∠EBC=∠ABE

查看试题解析
3.
如图，在△ABC中，点D，E分别在边AB，AC上，DE//BC，若BD=2AD，则（）

A、 $\frac{A D}{A B} = \frac{1}{2}$ B、 $\frac{A E}{E C} = \frac{1}{2}$ C、 $\frac{A D}{E C} = \frac{1}{2}$ D、 $\frac{D E}{B C} = \frac{1}{2}$

查看试题解析
4.
如图，在△ABC中，AB=AC，BC=12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD=x，tan∠ACB=y，则（）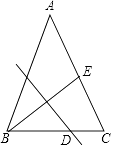

A、x﹣y²=3 B、2x﹣y²=9 C、3x﹣y²=15 D、4x﹣y²=21

查看试题解析

二、填空题

5.
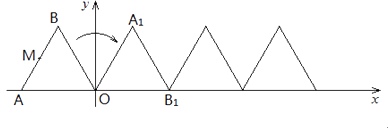
如图，正△ABO的边长为2，O为坐标原点，A在 $x$ 轴上，B在第二象限。△ABO沿 $x$ 轴正方向作无滑动的翻滚，经第一次翻滚后得△A₁B₁O，则翻滚3次后点B的对应点的坐标是；翻滚2017次后AB中点M经过的路径长为.

查看试题解析
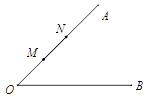
6.
如图，∠AOB=45°，点M，N在边OA上，OM=x，ON=x+4，点P是边OB上的点.若使点P，M，N构成等腰三角形的点P恰好有三个，则x的值是.

查看试题解析
7.
一副含 $30 °$ 和 $45 °$ 角的三角板 $A B C$ 和 $D E F$ 叠合在一起，边 $B C$ 与 $E F$ 重合， $B C = E F = 12 c m$ （如图1），点 $G$ 为边 $B C$ $(E F)$ 的中点，边 $F D$ 与 $A B$ 相交于点 $H$ ．现将三角板 $D E F$ 绕点 $G$ 按顺时针方向旋转（如图2），在 $∠ C G F$ 从 $0 °$ 到 $60 °$ 的变化过程中，点 $H$ 相应移动的路径长为．（结果保留根号）

查看试题解析
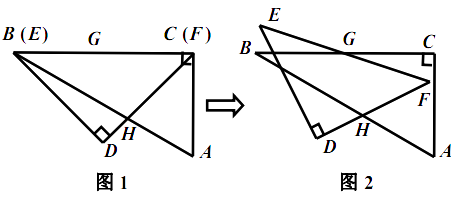8.
如图，在Rt△ABC中，∠BAC=90°，AB=15，AC=20，点D在边AC上，AD=5，DE⊥BC于点E，连结AE，则△ABE的面积等于．

查看试题解析

三、解答题

9.
问题背景
如图1，在正方形ABCD的内部，作∠DAE=∠ABF=∠BCG=∠CDH，根据三角形全等的条件，易得△DAE≌△ABF≌△BCG≌△CDH，从而得到四边形EFGH是正方形。
类比研究
如图2，在正△ABC的内部，作∠BAD=∠CBE=∠ACF，AD，BE，CF两两相交于D，E，F三点（D，E，F三点不重合）。

(1)、△ABD，△BCE，△CAF是否全等？如果是，请选择其中一对进行证明；

(2)、△DEF是否为正三角形？请说明理由；

(3)、进一步探究发现，△ABD的三边存在一定的等量关系，设 $B D = a$ ， $A D = b$ ， $A B = c$ ，请探索 $a$ ， $b$ ， $c$ 满足的等量关系。

查看试题解析
10.
已知△ABC，AB=AC，D为直线BC上一点，E为直线AC上一点，AD=AE，设∠BAD=α，∠CDE=β.

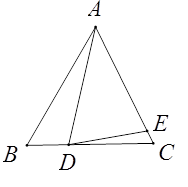(1)、如图，若点D在线段BC上，点E在线段AC上.
①如果∠ABC=60°，∠ADE=70°，那么α=°，β=°.②求α，β之间的关系式.

(2)、是否存在不同于以上②中的α，β之间的关系式？若存在，请求出这个关系式（求出一个即可）；若不存在，说明理由.

查看试题解析
11.
如图，已知等腰直角△ABC，点P是斜边BC上一点（不与B，C重合），PE是△ABP的外接圆⊙O的直径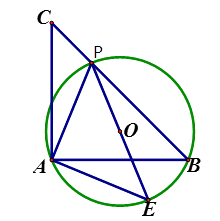

(1)、求证：△APE是等腰直角三角形；

(2)、若⊙O的直径为2，求 $P C^{2} + P B^{2}$ 的值

查看试题解析
12.
如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．

(1)、求证：△ADE∽△ABC；

(2)、若AD=3，AB=5，求 $\frac{A F}{A G}$ 的值．

查看试题解析
13.
如图，在五边形ABCDE中，∠BCD=∠EDC=90°，BC=ED，AC=AD．

(1)、求证：△ABC≌△AED；

(2)、当∠B=140°时，求∠BAE的度数．

查看试题解析