人教A版(2019)数学必修第一册5.1任意角和弧度制
试卷更新日期:2020-02-07 类型:同步测试
一、单选题
-
1. 将 角化为弧度制为( )A、 B、 C、 D、2. 将 弧度化成角度为( )A、 B、 C、 D、3. 将表的分针拨慢10分钟,则分针转过的角的弧度数是( )A、 B、 C、 D、4. 若角α=-4,则α的终边在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 与 终边相同的角的集合是( )A、
 B、
B、 C、
C、 D、
D、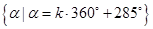 6. 若扇形的圆心角为2弧度,它所对的弧长为4,则扇形的面积为( )A、 B、 C、 D、7. 是( )A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角8. 下列角的终边位于第四象限的是( )A、
6. 若扇形的圆心角为2弧度,它所对的弧长为4,则扇形的面积为( )A、 B、 C、 D、7. 是( )A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角8. 下列角的终边位于第四象限的是( )A、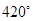 B、
B、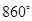 C、
C、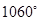 D、
D、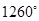 9. 若角 , ,( , ),则角 与 的终边的位置关系是( )A、重合 B、关于原点对称 C、关于 轴对称 D、关于 轴对称10. 若角 , ,则角 的终边落在( )A、第一或第三象限 B、第一或第二象限 C、第二或第四象限 D、第三或第四象限11. 下列命题中正确的是( )A、终边在 轴负半轴上的角是零角 B、三角形的内角必是第一、二象限内的角 C、不相等的角的终边一定不相同 D、若
9. 若角 , ,( , ),则角 与 的终边的位置关系是( )A、重合 B、关于原点对称 C、关于 轴对称 D、关于 轴对称10. 若角 , ,则角 的终边落在( )A、第一或第三象限 B、第一或第二象限 C、第二或第四象限 D、第三或第四象限11. 下列命题中正确的是( )A、终边在 轴负半轴上的角是零角 B、三角形的内角必是第一、二象限内的角 C、不相等的角的终边一定不相同 D、若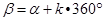 (
( 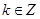 ),则 与 β 终边相同
12. 已知角 是第二象限角,那么角 是( ).A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第二、三象限13. 已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )A、 B、 C、 D、14. 时钟的分针在1点到3点20分这段时间里转过的弧度数为( )A、 B、 C、 D、
),则 与 β 终边相同
12. 已知角 是第二象限角,那么角 是( ).A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第二、三象限13. 已知2弧度的圆心角所对的弦长为2,那么这个圆心角所对的弧长为( )A、 B、 C、 D、14. 时钟的分针在1点到3点20分这段时间里转过的弧度数为( )A、 B、 C、 D、二、填空题
-
15. 在单位圆中, 的圆心角所对的弧长为.16. 若扇形圆心角为 ,扇形面积为 ,则扇形半径为.17. 若扇形的周长是 ,圆心角是2(rad),则扇形的面积是 .18. 已知扇形的周长是4cm,面积是1cm2 , 则扇形的圆心角的弧度数是 .19. 已知﹣990°<α<﹣630°,且α与120°角终边相同,则α= .20.
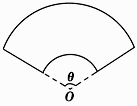
如图,写出终边落在阴影部分的角α的集合(含边界) .
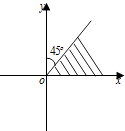 21. 若角α和β的终边关于直线x+y=0对称,且α=﹣ ,则角β的集合是22. 《九章算术》是中国古代数学名著,其对扇形田面积给出“以径乘周四而一”的算法与现代数学的算法一致,根据这一算法解决下列问题:现有一扇形田,下周长(弧长)为20米,径长(两段半径的和)为24米,则该扇形田的面积为平方米.
21. 若角α和β的终边关于直线x+y=0对称,且α=﹣ ,则角β的集合是22. 《九章算术》是中国古代数学名著,其对扇形田面积给出“以径乘周四而一”的算法与现代数学的算法一致,根据这一算法解决下列问题:现有一扇形田,下周长(弧长)为20米,径长(两段半径的和)为24米,则该扇形田的面积为平方米.三、解答题
-
23. 把下列各角的弧度化为角度或把角度化为弧度:(1)﹣135° (2) .24. 在角的集合{α|α=k•90°+45°,k∈Z}中:(1)、有几种终边不相同的角?(2)、有几个适合不等式﹣360°<α<360°的角?(3)、写出其中是第二象限角的一般表示法.25. 写出如图所示阴影部分的角α的范围.