2016-2017学年江西省新余市高一下学期期末数学试卷（文科）

试卷更新日期：2017-08-09 类型：期末考试

进入出卷网下载

一、选择题

1. $s i n \frac{2017}{4} π$ 等于（）

A、1 B、﹣1 C、 $\frac{\sqrt{2}}{2}$ D、 $- \frac{\sqrt{2}}{2}$

查看试题解析
2. 已知cos（α﹣π）=﹣ $\frac{5}{13}$ ，且α是第四象限角，则sin（﹣2π+α）=（）

A、﹣ $\frac{12}{13}$ B、 $\frac{12}{13}$ C、± $\frac{12}{13}$ D、 $\frac{5}{12}$

查看试题解析
3. 如图一铜钱的直径为32毫米，穿径（即铜钱内的正方形小孔边长）为8毫米，现向该铜钱内随机地投入一粒米（米的大小忽略不计），则该粒米未落在铜钱的正方形小孔内的概率为（）

A、 $\frac{1}{4 π}$ B、 $1 - \frac{1}{4 π}$ C、 $\frac{1}{2 π}$ D、 $1 - \frac{1}{6 π}$

查看试题解析
4. 已知 $\vec{a}$ =（﹣2，1）， $\vec{b}$ =（k，﹣3）， $\vec{c}$ =（1，2），若（ $\vec{a}$ ﹣2 $\vec{b}$ ）⊥ $\vec{c}$ ，则| $\vec{b}$ |=（）

A、 $3 \sqrt{5}$ B、3 $\sqrt{2}$ C、 $2 \sqrt{5}$ D、 $\sqrt{10}$

查看试题解析
5. 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b分别为14，18，则输出的a=（）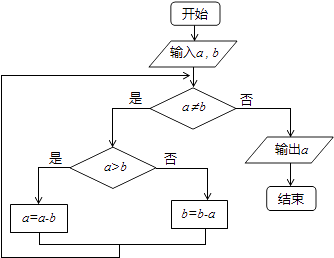

A、0 B、2 C、4 D、14

查看试题解析
6. 某初级中学领导采用系统抽样方法，从该校预备年级全体800名学生中抽50名学生做牙齿健康检查．现将800名学生从1到800进行编号，求得间隔数k= $\frac{800}{50}$ =16，即每16人抽取一个人．在1～16中随机抽取一个数，如果抽到的是7，则从33～48这16个数中应取的数是（）

A、40 B、39 C、38 D、37

查看试题解析
7. 直线l：x+y+a=0与圆C：x²+y²=3截得的弦长为 $\sqrt{3}$ ，则a=（）

A、 $\pm \frac{3}{2}$ B、 $\pm 3 \sqrt{2}$ C、±3 D、 $\pm \frac{3}{2} \sqrt{2}$

查看试题解析
8. 要得到y= $\sqrt{3}$ cos²x+sinxcosx的图象，只需把y=sin2x的图象上所有点（）

A、向左平移 $\frac{π}{6}$ 个单位，再向上移动 $\frac{\sqrt{3}}{2}$ 个单位 B、向左平移 $\frac{π}{3}$ 个单位，再向上移动 $\frac{\sqrt{3}}{2}$ 个单位 C、向右平移 $\frac{π}{6}$ 个单位，再向下移动 $\frac{\sqrt{3}}{2}$ 个单位 D、向右平移 $\frac{π}{3}$ 个单位，再向下移动 $\frac{\sqrt{3}}{2}$ 个单位

查看试题解析
9. 已知函数 $f (x) = s i n (ω x + \frac{π}{3}) (ω > 0)$ ，若 $f (\frac{π}{6}) = f (\frac{π}{3})$ 且f（x）在区间 $(\frac{π}{6} ， \frac{π}{3})$ 上有最小值，无最大值，则ω的值为（）

A、 $\frac{2}{3}$ B、 $\frac{5}{3}$ C、 $\frac{14}{3}$ D、 $\frac{38}{3}$

查看试题解析
10. 已知函数 $f (x) = 2 a s i n (2 x + \frac{π}{6}) + b$ 的定义域为 $[0 ， \frac{π}{2}]$ ，值域为[﹣5，1]，则函数g（x）=a^bx⁺⁷在[b，a]上，（）

A、有最大值2 B、有最小值2 C、有最大值1 D、有最小值1

查看试题解析
11. 在△ABC中，∠ABC=120°，BA=2，BC=3，D，E是线段AC的三等分点，则 $\vec{B D}$ • $\vec{B E}$ 的值为（）

A、 $\frac{65}{9}$ B、 $\frac{11}{9}$ C、 $\frac{41}{9}$ D、﹣ $\frac{13}{9}$

查看试题解析
12. 已知函数f（x）=cos² $\frac{ω x}{2}$ + $\frac{\sqrt{3}}{2}$ sinωx﹣ $\frac{1}{2}$ （ω＞0），x∈R，若f（x）在区间（π，2π）内没有零点，则ω的取值范围是（）

A、（0， $\frac{5}{12}$ ] B、（0， $\frac{5}{12}$ ]∪[ $\frac{5}{6}$ ， $\frac{11}{12}$ ） C、（0， $\frac{5}{6}$ ] D、（0， $\frac{5}{12}$ ]∪[ $\frac{5}{6}$ ， $\frac{11}{12}$ ]

查看试题解析

二、填空题

13. 弧长为3π，圆心角为135°的扇形半径为，面积为．

查看试题解析
14. y=Asin（ωx+φ）（ω＞0，φ∈（0，π）的图象的一段如图所示，它的解析式是．

查看试题解析
15. 已知f（tanx）=cos2x，则f（ $\frac{\sqrt{3}}{2}$ ）的值是．

查看试题解析
16. 设函数y=f（x）在区间上[0，1]的图象是连续不断的一条曲线，且恒有0≤f（x）≤1，可以用随机模拟方法近似计算出曲线y=f（x）及直线x=0，x﹣1=0，y=0所围成部分的面积S，先产生两组（每组N个）区间[0，1]上的均匀随机数X₁ ， X₂ ， X₃ ， X_N和y₁ ， y₂ ， y₃ ， y_N ，由此得到N个点（x_i ， y_i）（i=1，2，3N，再数出其中满足y_i≤f（x_i）（i=1，2，3，N）的点数N₁ ，那么由随机方法可以得到S的近似值为．

查看试题解析

三、解答题

17. 已知 $\vec{a}$ =（1，2）， $\vec{b}$ =（﹣3，2），当k为何值时，

(1)、k $\vec{a} + \vec{b}$ 与 $\vec{a} - 3 \vec{b}$ 垂直？

(2)、k $\vec{a} + \vec{b}$ 与 $\vec{a} - 3 \vec{b}$ 夹角为钝角？

查看试题解析
18. 某商区停车场临时停车按时段收费，收费标准为：每辆汽车一次停车不超过1小时收费6元，超过1小时的部分每小时收费8元（不足1小时的部分按1小时计算）．现有甲、乙二人在该商区临时停车，两人停车都不超过4小时．
（Ⅰ）若甲停车1小时以上且不超过2小时的概率为 $\frac{1}{3}$ ，停车付费多于14元的概率为 $\frac{5}{12}$ ，求甲停车付费恰为6元的概率；
（Ⅱ）若每人停车的时长在每个时段的可能性相同，求甲、乙二人停车付费之和为36元的概率．

查看试题解析
19. 已知函数 $f (x) = s i n (2 x + \frac{π}{6}) + s i n (2 x - \frac{π}{6})$ +cos2x+a（a∈R，a为常数）．
（Ⅰ）求函数的最小正周期；
（Ⅱ）求函数的单调递减区间；
（Ⅲ）若 $x \in [0 ， \frac{π}{2}]$ 时，f（x）的最小值为﹣2，求a的值．

查看试题解析
20. 某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年销售量y（单位：t）和年利润z（单位：千元）的影响．对近8年的年宣传费x_i和年销售量y_i（i=1，2，8）数据作了初步处理，
得到下面的散点图及一些统计量的值．
$\bar{x}$
$\bar{y}$
$\bar{w}$
$\sum_{i = 1}^{8} {(x_{i} - \bar{x})}^{2}$
$\sum_{i = 1}^{8} {(w_{i} - \bar{w})}^{2}$
$\sum_{i = 1}^{8} (x_{i} - \bar{x}) (y_{i} - \bar{y})$
$\sum_{i = 1}^{8} (w_{i} - \bar{w}) (y_{i} - \bar{y)}$
46.6
563
6.8
289.8
1.6
1469
108.8
其中w_i= $\sqrt{x_{i}}$ ， $\bar{w}$ = $\frac{1}{8} \sum_{i = 1}^{8} w_{i}$
（Ⅰ）根据散点图判断，y=a+bx与y=c+d $\sqrt{x}$ 哪一个适宜作为年销售量y关于年宣传费x的回归方程类型？（给出判断即可，不必说明理由）
（Ⅱ）根据（Ⅰ）的判断结果及表中数据，建立y关于x的回归方程；
（Ⅲ）已知这种产品的年利润z与x、y的关系为z=0.2y﹣x．根据（Ⅱ）的结果回答下列问题：
（i）年宣传费x=49时，年销售量及年利润的预报值是多少？
（ii）年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据（u₁ ， v₁），（u₂ ， v2），（u_n ， v_n），其回归直线v=α+βμ的斜率和截距的最小二乘估计分别为： $\hat{β}$ = $\frac{\sum_{i = 1}^{n} (u_{i} - \bar{u}) (v_{i} - \bar{v})}{\sum_{i = 1}^{n} {(u_{i} - \bar{u})}^{2}}$ ， $\hat{α}$ = $\bar{v}$ ﹣ $\hat{β} \bar{u}$ ．

查看试题解析
21. 设 $\vec{a}$ = $(s i n^{2} \frac{π + 2 x}{4} ， c o s x + s i n x)$ ， $\vec{b}$ =（4sinx，cosx﹣sinx），f（x）= $\vec{a}$ • $\vec{b}$ ．

(1)、求函数f（x）的解析式；

(2)、已知常数ω＞0，若y=f（ωx）在区间 $[- \frac{π}{2} ， \frac{2 π}{3}]$ 是增函数，求ω的取值范围；

(3)、设集合A= ${x | \frac{π}{6} \leq x \leq \frac{2 π}{3}}$ ，B={x||f（x）﹣m|＜2}，若A⊆B，求实数m的取值范围．

查看试题解析
22. 将函数y=sinx的图象上所有点的横坐标缩短到原来的 $\frac{1}{2}$ 倍（纵坐标不变），再将所得的图象向左平移 $\frac{π}{6}$ 个单位长度后得到函数f（x）的图象

(1)、写出函数f（x）的解析式；

(2)、若对任意的x∈[﹣ $\frac{π}{6}$ ， $\frac{π}{12}$ ]，f²（x）﹣mf（x）﹣1≤0恒成立，求实数m的取值范围；

(3)、求实数a和正整数n，使得F（x）=f（x）﹣a在[0，nπ]上恰有2017个零点．

查看试题解析

$\bar{x}$	$\bar{y}$	$\bar{w}$	$\sum_{i = 1}^{8} {(x_{i} - \bar{x})}^{2}$	$\sum_{i = 1}^{8} {(w_{i} - \bar{w})}^{2}$	$\sum_{i = 1}^{8} (x_{i} - \bar{x}) (y_{i} - \bar{y})$	$\sum_{i = 1}^{8} (w_{i} - \bar{w}) (y_{i} - \bar{y)}$
46.6	563	6.8	289.8	1.6	1469	108.8