人教版数学八年级上册第13章 13.3.2等边三角形 同步练习
试卷更新日期:2017-08-09 类型:同步测试
一、单选题
-
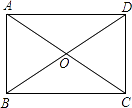
1. 如图,矩形ABCD的对角线AC=8cm,∠AOD=120°,则AB的长为( )
 A、 cm B、2cm C、2 cm D、4cm2. 如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( )
A、 cm B、2cm C、2 cm D、4cm2. 如图为正三角形ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( )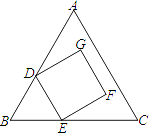 A、2 B、3 C、12﹣4 D、6 ﹣63. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )
A、2 B、3 C、12﹣4 D、6 ﹣63. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )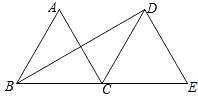 A、 B、 C、 D、4. 如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE,若AB=3,DE=1,则△EFC的面积为( )
A、 B、 C、 D、4. 如图为等边△ABC与正方形DEFG的重叠情形,其中D、E两点分别在AB、BC上,且BD=BE,若AB=3,DE=1,则△EFC的面积为( )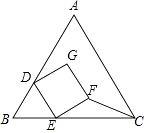 A、 B、1 C、 D、5. 如图,在正方形ABCD的内侧作等边△ADE,则∠EBC的度数为( )
A、 B、1 C、 D、5. 如图,在正方形ABCD的内侧作等边△ADE,则∠EBC的度数为( )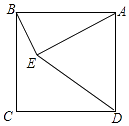 A、10° B、12.5° C、15° D、20°6. 点P在正方形ABCD内,且△PAB是等边三角形,那么∠DCP为( )A、15° B、18° C、22.5° D、30°7. 如图,已知等边△ABC,在平面上找一点P,使得△PAB、△PBC和△PAC都是等腰三角形,这样的点P的个数是( )
A、10° B、12.5° C、15° D、20°6. 点P在正方形ABCD内,且△PAB是等边三角形,那么∠DCP为( )A、15° B、18° C、22.5° D、30°7. 如图,已知等边△ABC,在平面上找一点P,使得△PAB、△PBC和△PAC都是等腰三角形,这样的点P的个数是( ) A、1 B、4 C、7 D、108. 如图,△ABC和△CDE都是等边三角形,则下列结论不成立的是( )
A、1 B、4 C、7 D、108. 如图,△ABC和△CDE都是等边三角形,则下列结论不成立的是( )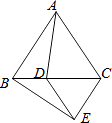 A、∠BDE=120° B、∠ACE=120° C、AB=BE D、AD=BE9. 如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )
A、∠BDE=120° B、∠ACE=120° C、AB=BE D、AD=BE9. 如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为( )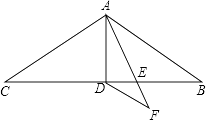 A、4.5 B、5 C、5.5 D、610. 下列说法正确的是( )A、完全重合的两个三角形全等 B、面积相等的两个三角形全等 C、所有的等边三角形全等 D、形状相同的两个三角形全等11. 下列说法正确的是( )A、周长相等的两个三角形全等 B、面积相等的两个三角形全等 C、完全重合的两个三角形全等 D、所有的等边三角形全等12. 如图,在正方形ABCD内部作等边三角形BCE,则∠AEB的度数为( )
A、4.5 B、5 C、5.5 D、610. 下列说法正确的是( )A、完全重合的两个三角形全等 B、面积相等的两个三角形全等 C、所有的等边三角形全等 D、形状相同的两个三角形全等11. 下列说法正确的是( )A、周长相等的两个三角形全等 B、面积相等的两个三角形全等 C、完全重合的两个三角形全等 D、所有的等边三角形全等12. 如图,在正方形ABCD内部作等边三角形BCE,则∠AEB的度数为( )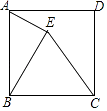 A、60° B、65° C、70° D、75°
A、60° B、65° C、70° D、75°二、填空题
-
13. 如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.当点E、F在BC、CD上滑动时,则△CEF的面积最大值是 .
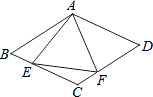 14. 如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP= .
14. 如图,四边形ABCD为正方形,△BPC为等边三角形,连接PD、BD,则∠BDP= .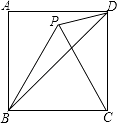 15. 如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于 .
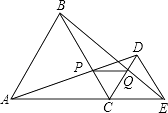
15. 如图:∠DAE=∠ADE=15°,DE∥AB,DF⊥AB,若AE=8,则DF等于 . 16. 如图,D、E分别是等边三角形ABC的两边AB、AC上的点,且AD=CE,BE,DC相交于点P,则∠BPD的度数为 .
16. 如图,D、E分别是等边三角形ABC的两边AB、AC上的点,且AD=CE,BE,DC相交于点P,则∠BPD的度数为 .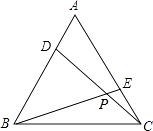 17. 如图,∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
17. 如图,∠MON=30°,点A1 , A2 , A3 , …在射线ON上,点B1 , B2 , B3 , …在射线OM上,△A1B1A2 , △A2B2A3 , △A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
三、解答题
-
18. 如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.
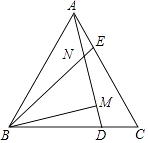
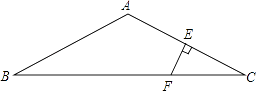 19. △ABD和△AEC都是等边三角形,连CD、BE,若BE=6,求DC的长.
19. △ABD和△AEC都是等边三角形,连CD、BE,若BE=6,求DC的长.
四、综合题
-
20. 如图1,在四边形ABCD中,DC∥AB,AD=BC,BD平分∠ABC.
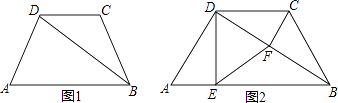 (1)、求证:AD=DC;(2)、如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.
(1)、求证:AD=DC;(2)、如图2,在上述条件下,若∠A=∠ABC=60°,过点D作DE⊥AB,过点C作CF⊥BD,垂足分别为E、F,连接EF.判断△DEF的形状并证明你的结论.