人教版数学八年级上册第13章 13.2.1作轴对称图形 同步练习
试卷更新日期:2017-08-09 类型:同步测试
一、单选题
-
1. 观察下图中各组图形,其中不是轴对称的是( )A、
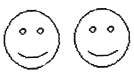
B、
B、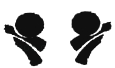
C、
C、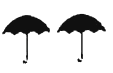
D、
D、
2. 作已知点关于某直线的对称点的第一步是( )A、过已知点作一条直线与已知直线相交 B、过已知点作一条直线与已知直线垂直 C、过已知点作一条直线与已知直线平行 D、不确定3. 下面四个图案中,既包含图形的旋转,又有图形的轴对称的设计是( )
2. 作已知点关于某直线的对称点的第一步是( )A、过已知点作一条直线与已知直线相交 B、过已知点作一条直线与已知直线垂直 C、过已知点作一条直线与已知直线平行 D、不确定3. 下面四个图案中,既包含图形的旋转,又有图形的轴对称的设计是( )
A、 B、
B、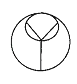 C、
C、 D、
D、 4. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )A、
4. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )A、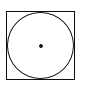 B、
B、 C、
C、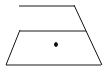 D、
D、 5. 我国主要银行的商标设计基本上都融入了中国古代钱币的图案,如图是我国四个银行的商标图案,其中是轴对称图形的有( )
5. 我国主要银行的商标设计基本上都融入了中国古代钱币的图案,如图是我国四个银行的商标图案,其中是轴对称图形的有( ) A、①②③ B、①②④ C、①③④ D、②③④6. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A、①②③ B、①②④ C、①③④ D、②③④6. 如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )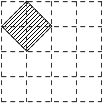 A、2种 B、3种 C、4种 D、5种7. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用轴对称知识的是( )A、
A、2种 B、3种 C、4种 D、5种7. 在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用轴对称知识的是( )A、 B、
B、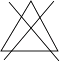 C、
C、 D、
D、 8. 在下列图形中,只利用没有刻度的直尺将无法作出其对称轴的是( )A、矩形 B、菱形 C、等腰梯形 D、正六边形9. 如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( )
8. 在下列图形中,只利用没有刻度的直尺将无法作出其对称轴的是( )A、矩形 B、菱形 C、等腰梯形 D、正六边形9. 如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( ) A、5 B、6 C、4 D、710. 如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( )
A、5 B、6 C、4 D、710. 如图,正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形涂黑一个,使整个图案构成一个轴对称图形,那么涂法共有( ) A、2种 B、3种 C、4种 D、5种
A、2种 B、3种 C、4种 D、5种二、填空题
-
11. 如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有个.
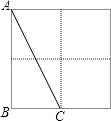 12. 如图,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有个,它们分别是 .
12. 如图,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有个,它们分别是 .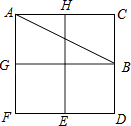 13. 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有种,请一一画出来.
13. 如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的方法有种,请一一画出来. 14. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种.
14. 在如图的方格纸上画有2条线段,若再画1条线段,使图中的三条线段组成一个轴对称图形,则这条线段的画法最多有种.
三、作图题
-
15. 如图,在方格纸上画出了一棵树的一半,请你以树干l为对称轴画出树的另一半.
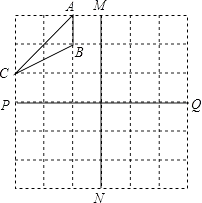
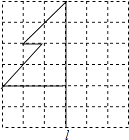 16. 已知:如图△ABC.
16. 已知:如图△ABC.①画出△A1B1C1 , 使△A1B1C1和△ABC关于直线MN成轴对称;
②画出△A2B2C2 , 使△A2B2C2和△A1B1C1关于直线PQ成轴对称;
③△ABC与△A2B2C2成轴对称吗?
四、解答题
-
17.
如图,△ABC中,点A(﹣2,1)、B(﹣3,4)C(﹣5,2)均在格点上.在所给直角坐标系中解答下列问题:
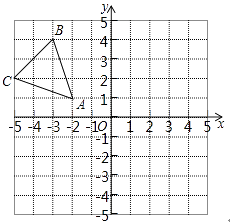
将△ABC平移得△A1B1C1使得点B的对应点B1与原点O重合,在所给直角坐标系中画出图形;在图中画出△ABC关于y轴对称的△A2B2C2 , 并写出A2、B2、C2的坐标;在x轴上找一点P,使得△PAB2的周长最小,请直接写出点P的坐标.
五、综合题
-
18. 有一张图纸被损坏,但上面有如图所示的两个标志点A(﹣3,1),B(﹣3,﹣3)可见,而主要建筑C(3,2)破损,
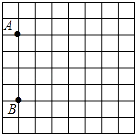 (1)、请通过建立直角坐标系找到图中C点的位置;(2)、请作出三角形ABC关于y轴对称的图形三角形A1B1C1;(3)、请求出三角形ABC的周长和面积.19. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1).
(1)、请通过建立直角坐标系找到图中C点的位置;(2)、请作出三角形ABC关于y轴对称的图形三角形A1B1C1;(3)、请求出三角形ABC的周长和面积.19. 如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1). (1)、在图中作出△ABC关于x轴对称的△A′B′C′;(2)、写出A′、B′、C′三点的坐标(直接写答案);(3)、在(1)(2)条件下,连接OAB′三点,求△OAB′的面积.20. 如图,在11×11的正方形网格中,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)、在图中作出△ABC关于x轴对称的△A′B′C′;(2)、写出A′、B′、C′三点的坐标(直接写答案);(3)、在(1)(2)条件下,连接OAB′三点,求△OAB′的面积.20. 如图,在11×11的正方形网格中,网格中有一个格点△ABC(即三角形的顶点都在格点上). (1)、在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1 , B与B1 , C与C1相对应);(2)、在直线l上找一点P,使得△PAC的周长最小;(3)、在(1)问的结果下,连接BB1、CC1 , 求四边形BB1C1C的面积.
(1)、在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1 , B与B1 , C与C1相对应);(2)、在直线l上找一点P,使得△PAC的周长最小;(3)、在(1)问的结果下,连接BB1、CC1 , 求四边形BB1C1C的面积.
-