人教版数学八年级上册第12章 12.3角的平分线的性质 同步练习
试卷更新日期：2017-08-09 类型：同步测试
一、单选题
-
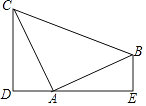
1. 如图，在四边形ABCD中，∠A=90°，AD=4，BC=5，对角线BD平分∠ABC，则△BCD的面积为（ ）
A、10 B、12 C、20 D、无法确定2. 如图，在Rt△ABC中，∠C=90°，BD是角平分线，若CD=m，AB=2n，则△ABD的面积是（ ）
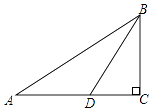A、mn B、5mn C、7mn D、6mn3.如图，△ABC中，∠C = 90°，AD是∠BAC的平分线，DE⊥AB于E，若DE = 8cm，DB = 10cm则BC等于（ ）
A、14cm B、16cm C、18cm D、20cm4. 下列说法错误的是（ ）A、角平分线上的点到角的两边的距离相等 B、直角三角形斜边上的中线等于斜边的一半 C、菱形的对角线相等 D、平行四边形是中心对称图形5. 如图，有A、B、C三个居民小区的位置成三角形，现决定在三个小区之间修建一个农贸市场，使农贸市场到三个小区的距离均相等，则超市应建在（ ）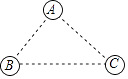
A、在三个内角角平分线的交点处 B、在三条高线的交点处 C、在三条中线的交点处 D、在三条边垂直平分线的交点处6. 如图，在△ABC中，点O是∠ABC的平分线与线段BC的垂直平分线的交点，OD⊥BC，OE⊥AC，OF⊥AB．垂足分别为D、E、F，则下列结论不一定成立的是（ ）
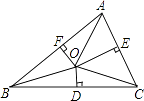A、OB=OC B、OD=OF C、OA=OB=OC D、BD=DC7. 如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于，且OD=4，△ABC的面积是（ ）
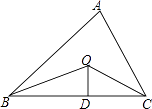A、25 B、84 C、42 D、218.如图，在Rt△ABC中，∠C=90°，AD平分∠BAC，若AC=6，BC=8，则CD的长为（ ）
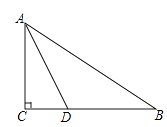
A、2 B、3 C、4 D、59. 如图，PD⊥AB，PE⊥AC，垂足分别为D、E，且PD=PE，则△APD与△APE全等的理由是（ ）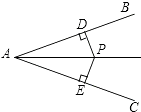
A、SAS B、AAS C、SSS D、HL10. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（ ）
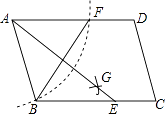A、4 B、6 C、8 D、1011.如图，在▱ABCD中，AB=4，AD=7，∠ABC的平分线BE交AD于点E ， 则DE的长是（ ）
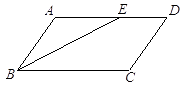A、4 B、3 C、3.5 D、2二、填空题
-
12. 直角三角形中两锐角平分线相交所成的角的度数是 ．13. 如图，BD平分∠ABC，DE⊥AB于E，DF⊥BC于F，AB=6，BC=8．若S△ABC=28，则DE= ．
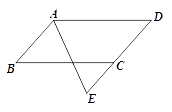
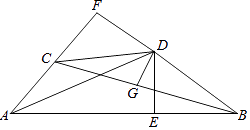
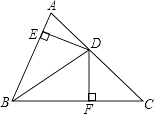14. 如图，△ABC中，D是AB的中点，DE⊥AB，∠ACE+∠BCE=180°，EF⊥AC交AC于F，AC=12，BC=8，则AF= ．
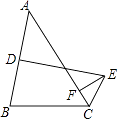15. 如图：∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于 ．
16. 如图，在△ABC中，∠A=90，BD是角平分线，若AD=m，BC=n，则△BDC的面积为 ．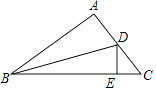
三、解答题
-
17. 如图：AD是∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，连接E、F，
求证：AD是EF的垂直平分线．
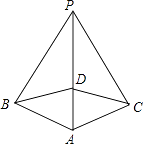
18. 如图，△ABC中，AB=AC，M是BC的中点，过点M作ME⊥AB、MF⊥AC，垂足分别为E、F．求证：ME=MF．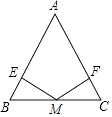
19. 如图，已知PB⊥AB，PC⊥AC，且PB=PC，D是AP上的一点，求证：BD=CD．
