人教版数学八年级上册第11章 11.3.2多边形的内角和 同步练习

试卷更新日期：2017-08-09 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图，一块四边形绿化园地，四角都做有半径为R的圆形喷水池，则这四个喷水池占去的绿化园地的面积为（   ）

    A、2πR2 B、4πR2 C、πR2 D、不能确定

    查看试题解析

  • 2. 一个凸n边形，其每个内角都是140°，则n的值为（　　）

    A、6 B、7 C、8 D、9

    查看试题解析

  • 3. 已知一个多边形的最小的外角是60°，其余外角依次增加20°，则这个多边形的边数为（   ）
    A、6 B、5 C、4 D、3

    查看试题解析

  • 4. 一个多边形的内角和等于1260°，则从此多边形一个顶点引出的对角线有（   ）
    A、4条 B、5条 C、6条 D、7条

    查看试题解析

  • 5. 某同学在计算某n边形的内角和时，不小心少输入一个内角，得到和为2005°．则n等于（   ）
    A、11 B、12 C、13 D、14

    查看试题解析

  • 6.

    如图，小明在操场上从A点出发，沿直线前进10米后向左转40°，再沿直线前进10米后，又向左转40°，照这样走下去，他第一次回到出发地A点时，一共走了（   ）米．

    A、70 B、80 C、90 D、100

    查看试题解析

  • 7. 正五边形的每个内角都等于（   ）
    A、60° B、90° C、108° D、120°

    查看试题解析

  • 8. 下列各角不是多边形的内角的是（   ）
    A、180° B、540° C、1900° D、1080°

    查看试题解析

  • 9. 若n边形的内角和为1440°，则n的值是（   ）
    A、8 B、9 C、10 D、11

    查看试题解析

  • 10. 如果一个多边形的每一个内角都是135°，那么这个多边形的边数是（   ）
    A、5 B、6 C、8 D、10

    查看试题解析

  • 11. 已知正多边形的每个内角均为108°，则这个正多边形的边数为（   ）

    A、3 B、4 C、5 D、6

    查看试题解析

  • 12. 下列结论：①一个三角形的3个外角的度数之比为2：3：4，则与之相应的3个内角度数之比为5：3：1；②在△ABC中，若∠A=2∠B=3∠C，则△ABC为直角三角形；③一个多边形的边数每增加一条，这个多边形的内角和就增加180°；④一个五边形最多有3个内角是直角；⑤两条直线被第三条直线所截，同位角的角平分线互相平行．其中正确结论有（   ）
    A、2个 B、3个 C、4个 D、5个

    查看试题解析

二、填空题

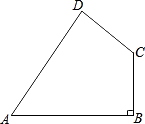
  • 13. 如果一个多边形的内角和等于它外角和的3倍，则这个多边形的边数是 ．

    查看试题解析

  • 14. 如图，四边形ABCD中，AB⊥BC，∠A=∠C=100°，则∠D的度数为度．

    查看试题解析

  • 15.

    把正三角形、正四边形、正五边形按如图所示的位置摆放，若∠1=52°，∠2=18°，则∠3= ．

    查看试题解析

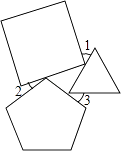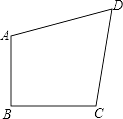
  • 16. 如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=

    度．

    查看试题解析

三、解答题

  • 17. 若一个多边形的每一个内角都等于120°，求该多边形的边数．

    查看试题解析

  • 18. 一个多边形的外角和是内角和的 27 ，求这个多边形的边数．

    查看试题解析

  • 19. 已知一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数．

    查看试题解析

  • 20. 如图，五边形ABCDE的内角都相等，且∠1=∠2，∠3=∠4，求x的值．

    查看试题解析

  • 21. 如图，四边形ABCD中，AB=20，BC=15，CD=7，AD=24，∠B=90°，求证：∠A+∠C=180°．

    查看试题解析