人教版数学八年级上册第11章 11.2.2三角形的外角 同步练习
试卷更新日期:2017-08-09 类型:同步测试
一、单选题
-
1. 如图,已知D为BC上一点,∠B=∠1,∠BAC=78°,则∠2=( )
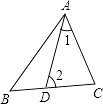 A、78° B、80° C、50° D、60°2. 如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( )
A、78° B、80° C、50° D、60°2. 如图,已知∠BOF=120°,则∠A+∠B+∠C+∠D+∠E+∠F为多少度( ) A、360° B、720° C、540° D、240°3. 下列说法中不正确的是( )A、三角形按边分可分为不等边三角形、等腰三角形 B、等腰三角形的内角可能是钝角或直角 C、三角形外角一定是钝角 D、三角形的中线把三角形分成面积相等的两部分4. 如图:∠2 大于∠1的是( )A、
A、360° B、720° C、540° D、240°3. 下列说法中不正确的是( )A、三角形按边分可分为不等边三角形、等腰三角形 B、等腰三角形的内角可能是钝角或直角 C、三角形外角一定是钝角 D、三角形的中线把三角形分成面积相等的两部分4. 如图:∠2 大于∠1的是( )A、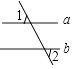 B、
B、 C、
C、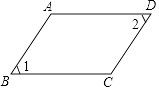 D、
D、 5. 已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是( )A、钝角 B、锐角 C、直角 D、无法确定6. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )
5. 已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是( )A、钝角 B、锐角 C、直角 D、无法确定6. 如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )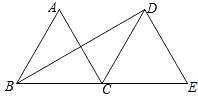 A、 B、 C、 D、7. 如图是一副三角尺叠放的示意图,则∠α的度数为( )
A、 B、 C、 D、7. 如图是一副三角尺叠放的示意图,则∠α的度数为( ) A、75° B、45° C、30° D、15°8. 一副三角板如图叠放在一起,则图中∠α的度数为( )
A、75° B、45° C、30° D、15°8. 一副三角板如图叠放在一起,则图中∠α的度数为( )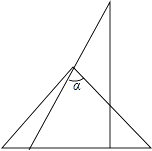 A、75° B、60° C、65° D、55°9. 已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A、75° B、60° C、65° D、55°9. 已知如图,△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( ) A、315° B、270° C、180° D、135°10. 如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形.
A、315° B、270° C、180° D、135°10. 如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形.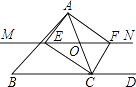 A、30° B、45° C、60° D、90°11. 下列结论:①一个三角形的3个外角的度数之比为2:3:4,则与之相应的3个内角度数之比为5:3:1;②在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形;③一个多边形的边数每增加一条,这个多边形的内角和就增加180°;④一个五边形最多有3个内角是直角;⑤两条直线被第三条直线所截,同位角的角平分线互相平行.其中正确结论有( )A、2个 B、3个 C、4个 D、5个12.
A、30° B、45° C、60° D、90°11. 下列结论:①一个三角形的3个外角的度数之比为2:3:4,则与之相应的3个内角度数之比为5:3:1;②在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形;③一个多边形的边数每增加一条,这个多边形的内角和就增加180°;④一个五边形最多有3个内角是直角;⑤两条直线被第三条直线所截,同位角的角平分线互相平行.其中正确结论有( )A、2个 B、3个 C、4个 D、5个12.如图,在直角三角形ABC中,CD是斜边AB上的中线 ,若∠A=20°,则∠BDC=( )
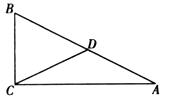 A、30° B、40° C、45° D、60°
A、30° B、40° C、45° D、60°二、填空题
-
13. 将一副三角板按图中方式叠放,则角α的度数为 .
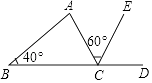
 14. 如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A
14. 如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=60°,则∠A=度.
 15. 如图,△ABC中,DE是∠ADC角平分线,若已知∠B=50°,∠BAD=60°,则∠CDE= .
15. 如图,△ABC中,DE是∠ADC角平分线,若已知∠B=50°,∠BAD=60°,则∠CDE= .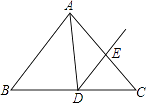 16. 如图,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,则∠CDE=度.
16. 如图,在△ABC中,∠B=∠C,∠BAD=34°,且∠ADE=∠AED,则∠CDE=度. 17. 如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF= .
17. 如图所示,∠B=67°,∠ACB=74°,∠AED=48°,则∠BDF= .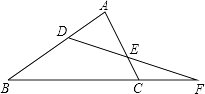
三、计算题
-
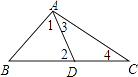
18. 如图,在△ABC中,D是BC上的一点,∠1=∠2,∠3=∠4,∠B=40°,求∠BAC的度数.
 19. 如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,∠B=30°,∠E=20°,求∠ACE和∠BAC的度数.
19. 如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,∠B=30°,∠E=20°,求∠ACE和∠BAC的度数.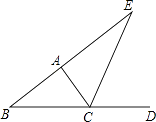 20. 如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
20. 如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.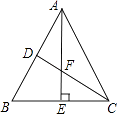 21. 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
21. 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.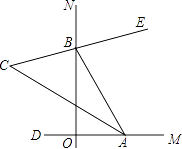
四、综合题
-
22. 已知△ABC中,∠A=30°.(1)、如图①,∠ABC、∠ACB的角平分线交于点O,则∠BOC=°.
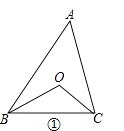 (2)、如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2 , 则∠BO2C=°.
(2)、如图②,∠ABC、∠ACB的三等分线分别对应交于O1、O2 , 则∠BO2C=°. (3)、如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示).
(3)、如图③,∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1(内部有n﹣1个点),求∠BOn﹣1C(用n的代数式表示).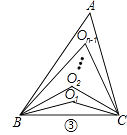 (4)、如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1 , 若∠BOn﹣1C=60°,求n的值.23. 在△ABC中,∠A=40°:
(4)、如图③,已知∠ABC、∠ACB的n等分线分别对应交于O1、O2…On﹣1 , 若∠BOn﹣1C=60°,求n的值.23. 在△ABC中,∠A=40°: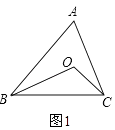 (1)、如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC;
(1)、如图(1)BO、CO是△ABC的内角角平分线,且相交于点O,求∠BOC; (2)、如图(2)BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;
(2)、如图(2)BO、CO是△ABC的外角角平分线,且相交于点O,求∠BOC;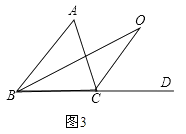 (3)、如图(3)BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;(4)、根据上述三问的结果,当∠A=n°时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).
(3)、如图(3)BO、CO分别是△ABC的一内角和一外角角平分线,且相交于点O,求∠BOC;(4)、根据上述三问的结果,当∠A=n°时,分别可以得出∠BOC与∠A有怎样的数量关系(只需写出结论).