陕西省西安市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-04 类型:期末考试
一、选择题(每题3分,共30分)
-
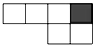
1. 的倒数是( )A、3 B、 C、 D、-32. 如图,需要添一个面折叠后,才能围成一个正方体,下图中黑色小正方形分别补画正确的是( )A、
 B、
B、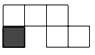 C、
C、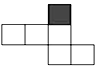 D、
D、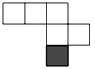 3. 西安市某区三月中旬每天平均空气质量指数(AQI)分别为:118,96, 60,82,56,69,86,112,108,94,为了描述这十天空气质量的变化情况,最适合用的统计图是( )A、折线统计图 B、条形统计图 C、频数分布直方图 D、扇形统计图4. 在国家“一带一路”倡议下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途经城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示应为( )A、0.13×105 B、1.3×104 C、1.3×105 D、13×1035. 下列描述不正确的是( )A、单项式 的系数是 ,次数是3次 B、用一个平面去截一个圆柱,截面的形状可能是一个长方形 C、过七边形的一个顶点有5条对角线 D、五棱柱有7个面,15条棱6. 已知,C是线段AB上的一点,不能确定C是线段AB中点的是( )A、AC+CB=AB B、AC= AB C、AB=2BC D、AC=BC7. 下列等式变形正确的是( )A、若-3x=5,则x= B、若 ,则2x+3(x-1)=1 C、若5x-6=2x+8,则5x+2x=8+6 D、若3(x+1)-2x=1则3x+3-2x=18. 已知关于x的多项式(2mx2+5x2+3x+1)-(6x2+3x)化简后不含x2项,则m的值是( )A、0 B、0.5 C、3 D、-2.59. 如图所示,已知直线AB,CD相交于O,OE平分∠COB,若∠EOB=55,则∠BOD的度数是( )
3. 西安市某区三月中旬每天平均空气质量指数(AQI)分别为:118,96, 60,82,56,69,86,112,108,94,为了描述这十天空气质量的变化情况,最适合用的统计图是( )A、折线统计图 B、条形统计图 C、频数分布直方图 D、扇形统计图4. 在国家“一带一路”倡议下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途经城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示应为( )A、0.13×105 B、1.3×104 C、1.3×105 D、13×1035. 下列描述不正确的是( )A、单项式 的系数是 ,次数是3次 B、用一个平面去截一个圆柱,截面的形状可能是一个长方形 C、过七边形的一个顶点有5条对角线 D、五棱柱有7个面,15条棱6. 已知,C是线段AB上的一点,不能确定C是线段AB中点的是( )A、AC+CB=AB B、AC= AB C、AB=2BC D、AC=BC7. 下列等式变形正确的是( )A、若-3x=5,则x= B、若 ,则2x+3(x-1)=1 C、若5x-6=2x+8,则5x+2x=8+6 D、若3(x+1)-2x=1则3x+3-2x=18. 已知关于x的多项式(2mx2+5x2+3x+1)-(6x2+3x)化简后不含x2项,则m的值是( )A、0 B、0.5 C、3 D、-2.59. 如图所示,已知直线AB,CD相交于O,OE平分∠COB,若∠EOB=55,则∠BOD的度数是( )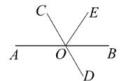 A、20° B、25° C、30° D、70°10. 甲、乙二人从相距21千米的两地同时出发,相向而行,120分钟相遇。甲每小时比乙多走500米,设乙的速度为x千米小时,下面所列方程正确的是( )A、2(x+0.5)+2x=21 B、2(x+500)+2x=21 C、120(x-500)+120x=21 D、120(x-0.5)+120x=21
A、20° B、25° C、30° D、70°10. 甲、乙二人从相距21千米的两地同时出发,相向而行,120分钟相遇。甲每小时比乙多走500米,设乙的速度为x千米小时,下面所列方程正确的是( )A、2(x+0.5)+2x=21 B、2(x+500)+2x=21 C、120(x-500)+120x=21 D、120(x-0.5)+120x=21二、填空题(每题3分,共12分)
-
11. 在数轴上与-2所对应的点相距4个单位长度的点表示的数是。12. 28.3375°=°'''
13. 若x=-1是方程2x+a=0的解,则a= 。14. 若|a-2|+( -b)2=0,则-ba=。三、解答题(共58分)
-
15. 作图题:
如图,已知线段a和b,请用直尺和圆规作出线段AC和AD,(不必写作法只需保留作图痕迹)
 (1)、使AC=2a+b(2)、使AD=2a-b16. 计算题:(1)、计算:8+(-3)2×(-2)(2)、计算:-14+16÷(-2)3-( )2×|-4|17. 解方程:(1)、2x-(2-x)=4(2)、18. 化简求值:
(1)、使AC=2a+b(2)、使AD=2a-b16. 计算题:(1)、计算:8+(-3)2×(-2)(2)、计算:-14+16÷(-2)3-( )2×|-4|17. 解方程:(1)、2x-(2-x)=4(2)、18. 化简求值:(-x2+xy-y2)-2(xy-3x2)+3(2y2-x),其中x=-1,y=-2
19. 某学校跳绳活动月即将开始,其中有一项为跳绳比赛,体育组为了了解七年级学生的训练情况,随机抽取了七年级部分学生进行1分钟跳绳测试,并将这些学生的测试成绩(即1分钟的个数,且这些测试成绩都在60~180范围内)分段后给出相应等级,具体为:测试成绩在60~90范围内的记为D级,90~120范围内的记为C级,120~150范围内的记为B级,150~180范围内的记为A级。现将数据整理绘制成如下两幅不完整的统计图,其中在扇形统计图中A级对应的圆心角为90°,请根据图中的信息解答下列问题: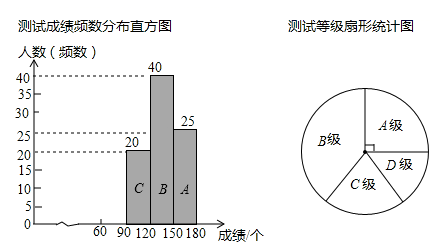 (1)、在扇形统计图中,求A级所占百分比;(2)、在这次测试中,求一共抽取学生的人数,并补全频数分布直方图;(3)、在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数。20. 如图,∠BOC=2∠AOC,OD是∠AOB的平分线,且∠COD=18°,求∠AOC的度数.
(1)、在扇形统计图中,求A级所占百分比;(2)、在这次测试中,求一共抽取学生的人数,并补全频数分布直方图;(3)、在(2)中的基础上,在扇形统计图中,求D级对应的圆心角的度数。20. 如图,∠BOC=2∠AOC,OD是∠AOB的平分线,且∠COD=18°,求∠AOC的度数.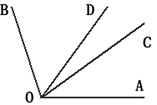 21. 计算:
21. 计算:已知|x|=3,|y|=2
(1)、当xy<0时,求x+y的值;(2)、求x-y的最大值。22. 为开展阳光体育活动,某班需要购买一批羽毛球拍和羽毛球,现了解情况如下:甲、乙两家商店出售同样品牌的羽毛球拍和羽毛球,羽毛球拍每副定价30元,羽毛球每盒定价5元,且两家都有优惠:甲店每买一副球拍赠一盒羽毛球;乙店全部按定价的9折优惠.
(1)、若该班需购买羽毛球拍5副,购买羽毛球x盒(不小于5盒)当购买多少盒羽毛球时,在两家商店购买所花的钱相等?(2)、若需购买10副羽毛球拍,30盒羽毛球,怎样购买更省钱?23. 如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=22,动点P从A点出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒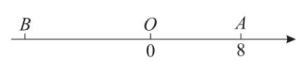 (1)、数轴上点B表示的数是;点P表示的数是(用含t的代数式表示)(2)、动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?(3)、若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN的长。
(1)、数轴上点B表示的数是;点P表示的数是(用含t的代数式表示)(2)、动点Q从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P、Q同时出发,问多少秒时P、Q之间的距离恰好等于2?(3)、若M为AP的中点,N为BP的中点,在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由,若不变,请你画出图形,并求出线段MN的长。