陕西省西安市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-04 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 在-1.414, ,π, ,3.21221222…3.14这些数中,无理数的个数为( )A、5 B、2 C、3 D、42. 下列各式运算正确的是( )A、 =±2 B、(-1)2=1 C、(-1)0=-1 D、 =-23. 甲、乙、丙、丁四个小组的同学分别参加了班里组织的中华古诗词知识竞赛,在相同条件下各小组的成绩情况如下表所示,若要从中选择出一个小组参加年级的比赛,那么应选( )
甲
乙
丙
丁
平均分
85
90
88
90
方差
3.5
3.5
4
4.2
A、甲组 B、乙组 C、丙组 D、丁组4. 平面直角坐标系中,点P(-2,3)关于x轴对称的点的坐标为( )A、(-2,-3) B、(2,-3) C、(-3,-2) D、(3,-2)5. 已知直线m∥n,将一块含30°角的直角三角板ABC,按如图所示方式放置,其中A,B两点分别落在直线m、n上,若∠1=25°,则∠2的度数是( ) A、25° B、30° C、35° D、55°6. 设点A(a,b)是正比例函数y= x图象上的任意一点,则下列等式一定成立的是( )A、2a+3b=0 B、2a-3b=0 C、3a-2b=0 D、3a+2b=07. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是4,9,1,4,则最大正方形E的面积是( )
A、25° B、30° C、35° D、55°6. 设点A(a,b)是正比例函数y= x图象上的任意一点,则下列等式一定成立的是( )A、2a+3b=0 B、2a-3b=0 C、3a-2b=0 D、3a+2b=07. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的边长分别是4,9,1,4,则最大正方形E的面积是( ) A、18 B、114 C、194 D、3248. 一次函数y=kx-k(k<0)的图象大致是( )A、
A、18 B、114 C、194 D、3248. 一次函数y=kx-k(k<0)的图象大致是( )A、 B、
B、 C、
C、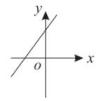 D、
D、 9. 甲、乙两地相距360千米,一轮船往返于甲、乙两地之间,顺流用18小时, 逆流用24小时,若设船在静水中的速度为x千米/时,水流速度为y千米/时,则下列方程组中正确的是( )A、 B、 C、 D、10. 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为( )
9. 甲、乙两地相距360千米,一轮船往返于甲、乙两地之间,顺流用18小时, 逆流用24小时,若设船在静水中的速度为x千米/时,水流速度为y千米/时,则下列方程组中正确的是( )A、 B、 C、 D、10. 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题(每题3分,共12分)
-
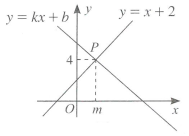
11. 数据-1,0,1,2,3的标准差为 。12. 如图,一次函数y=x+2与y=kx+b的图象相交于点P(m,4),则方程组 的解是.
 13. 如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE=。
13. 如图,在△ABC中,AB=AC,D、E两点分别在AC、BC上BD是∠ABC的平分线,DE∥AB,若BE=5cm,CE=3cm,则△CDE=。
三、解答题(共58分)
-
14. 计算题(1)、(2)、15. 解方程组(1)、(2)、16. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3)。
 (1)、①请在如图所示的网格平面内作出平面直角坐标系;
(1)、①请在如图所示的网格平面内作出平面直角坐标系;②请作出△ABC关于y轴对称的△A1B1C1;
(2)、点B的坐标是( , ),△ABC的面积是。17. 为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: (1)、补全频数分布直方图;(2)、本次调查学生参加户外活动时间的众数是 , 中位数是;(3)、本次调查学生参加户外活动的平均时间是否符合要求?18. 某城市对居民用水实行阶梯收费,每户每月用水量如果未超过20吨按每吨1.9元收费;每户每月用水量如果超过20吨,未超过的部分仍按每吨1.9元收费,超过的部分则按每吨2.8元收费.设某户每月的用水量为x吨,应收水费为y元。(1)、分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式。(2)、若该城市某户居民5月份水费平均为每吨2.2元,问该户居民5月份用水多少吨?19.
(1)、补全频数分布直方图;(2)、本次调查学生参加户外活动时间的众数是 , 中位数是;(3)、本次调查学生参加户外活动的平均时间是否符合要求?18. 某城市对居民用水实行阶梯收费,每户每月用水量如果未超过20吨按每吨1.9元收费;每户每月用水量如果超过20吨,未超过的部分仍按每吨1.9元收费,超过的部分则按每吨2.8元收费.设某户每月的用水量为x吨,应收水费为y元。(1)、分别写出每月用水量未超过20吨和超过20吨,y与x间的函数关系式。(2)、若该城市某户居民5月份水费平均为每吨2.2元,问该户居民5月份用水多少吨?19.已知:如图,在△ABC中,AD平分外角∠EAC,∠B=∠C.求证:AD∥BC.
 20. 如图,直线l1:y=-x+4分别与x轴,y轴交于点D,点A,直线l2:y= x+1与x轴交于点C,两直线l1 , l2相交于点B,连接AC。
20. 如图,直线l1:y=-x+4分别与x轴,y轴交于点D,点A,直线l2:y= x+1与x轴交于点C,两直线l1 , l2相交于点B,连接AC。 (1)、求点B的坐标和直线AC的解析式;(2)、求△ABC的面积。21. 某一天,水果经营户老刘用160元从水果批发市场批发猕猴桃和芒果共50千克,后到市场云卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:
(1)、求点B的坐标和直线AC的解析式;(2)、求△ABC的面积。21. 某一天,水果经营户老刘用160元从水果批发市场批发猕猴桃和芒果共50千克,后到市场云卖,已知猕猴桃和芒果当天的批发价和零售价如表所示:品名
猕猴桃
芒果
批发价(元/千克)
20
40
零售价(元/千克)
26
50
(1)、他购进的猕猴桃和芒果各多少千克?(2)、如果猕猴桃和芒果全部卖完,他能赚多少钱?22. 如图,已知直线l经过点A(1,0),B(0,2) (1)、求直线l的函数解析式(2)、如图,设点P是线段AB上一动点(不与A、B重合),将线段OP绕点O逆时针旋转90°至OQ,连结BO、PQ,PQ交y轴于点T,设点P的横坐标为t。当△OPQ的面积最小时,求点T的坐标。
(1)、求直线l的函数解析式(2)、如图,设点P是线段AB上一动点(不与A、B重合),将线段OP绕点O逆时针旋转90°至OQ,连结BO、PQ,PQ交y轴于点T,设点P的横坐标为t。当△OPQ的面积最小时,求点T的坐标。