江苏省苏州市2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-02-04 类型:期末考试
一、选择题 (本大题共有10小题,每小题3分,共30分.)
-
1. -8的绝对值为( )A、8 B、-8 C、 D、2. 将 用科学记数法表示为( )A、 B、 C、 D、3. 若 a>b ,则下列不等式中成立的是( )A、a+2<b+2 B、a-2<b-2 C、2a<2b D、-2a<-2b4. 下列关于0的说法正确的是( )A、0是正数 B、0是负数 C、0是有理数 D、0是无理数5. 下列立体图形中,俯视图是三角形的是( )A、
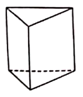 B、
B、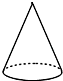 C、
C、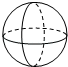 D、
D、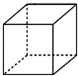 6. 如图,数轴上有A,B,C,D四个点,其中所对应的数的绝对值最大的点是( )
6. 如图,数轴上有A,B,C,D四个点,其中所对应的数的绝对值最大的点是( ) A、点A B、点B C、点C D、点D7. 如图,点C是AB的中点,点D是BC的中点,则下列等式中正确的有( )
A、点A B、点B C、点C D、点D7. 如图,点C是AB的中点,点D是BC的中点,则下列等式中正确的有( )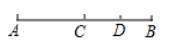
① ② ③ ④
A、1个 B、2个 C、3个 D、4个8. 一件毛衣先按成本提高50%标价,再以8折出售,获利70元,求这件毛衣的成本是多少元,若设成本是x元,可列方程为( )A、0.8x+70=(1+50%)x B、0.8 x-70=(1+50%)x C、x+70=0.8×(1+50%)x D、x-70=0.8×(1+50%)x9. 如图,已知 是直角,OM平分 ,ON平分 ,则 的度数是( ) A、30° B、45° C、50° D、60°10. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>26”为一次程序操作,如果程序操作进行了2次后停止,那么满足条件的所有整数x的和为( )
A、30° B、45° C、50° D、60°10. 运行程序如图所示,规定:从“输入一个值x”到“结果是否>26”为一次程序操作,如果程序操作进行了2次后停止,那么满足条件的所有整数x的和为( ) A、30 B、35 C、42 D、39
A、30 B、35 C、42 D、39二、填空题(本大题共8 小题,每小题3分,共24分)
-
11. 的相反数是 .12. 已知∠α=28°,则∠α的补角为°.13. 在数轴上,与-3表示的点相距4个单位的点所对应的数是 .14. 若 是关于x的方程 的解,则a的值为 .15. 将一张长方形纸条折成如图所示的图形,如果∠1=64°,那么∠2=°.
 16. 若 ,则 = .17. 已知 是关于x的不等式 的解,则m的取值范围为 .18. 一条数轴上有点A、B、C,其中点A、B表示的数分别是-16、9,现以点C为折点,将数轴向右对折,若点A对应的点A’落在点B的右边,并且A’B=3,则C点表示的数是 .
16. 若 ,则 = .17. 已知 是关于x的不等式 的解,则m的取值范围为 .18. 一条数轴上有点A、B、C,其中点A、B表示的数分别是-16、9,现以点C为折点,将数轴向右对折,若点A对应的点A’落在点B的右边,并且A’B=3,则C点表示的数是 .
三、解答题(本大题共10小题,共76分)
-
19. 计算:(1)、 ;(2)、 .20. 先化简,再求值:
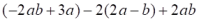 ,其中a=3,b=1. 21. 解方程:(1)、 ;(2)、 .22. 解不等式组: 并在数轴表示它的解集.
,其中a=3,b=1. 21. 解方程:(1)、 ;(2)、 .22. 解不等式组: 并在数轴表示它的解集.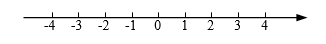 23. 如图,网格线的交点叫格点,格点P是 的边OB上的一点(请利用网格作图,保留作图痕迹)
23. 如图,网格线的交点叫格点,格点P是 的边OB上的一点(请利用网格作图,保留作图痕迹)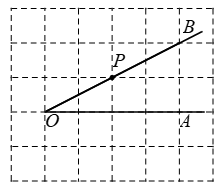 (1)、过点P画OB的垂线,交OA于点C;(2)、过点P画OA的垂线,垂足为H;(3)、线段PH的长度是点P到的距离,线段的长度是点C到直线OB的距离,因为所以线段PC,PH,OC这三条线段大小关系是(用“<”号连接).24. 把边长为1的10个相同正方体摆成如图的形式.
(1)、过点P画OB的垂线,交OA于点C;(2)、过点P画OA的垂线,垂足为H;(3)、线段PH的长度是点P到的距离,线段的长度是点C到直线OB的距离,因为所以线段PC,PH,OC这三条线段大小关系是(用“<”号连接).24. 把边长为1的10个相同正方体摆成如图的形式.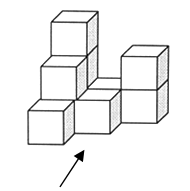 (1)、画出该几何体的主视图、左视图、俯视图;
(1)、画出该几何体的主视图、左视图、俯视图; (2)、试求出其表面积(包括向下的面);(3)、如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加个小正方体.25. 阳光集团新进了20台电视机和30台电饭煲,计划将这50台电器调配给下属的甲、乙两个商店销售,其中40台给甲商店,10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表:
(2)、试求出其表面积(包括向下的面);(3)、如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加个小正方体.25. 阳光集团新进了20台电视机和30台电饭煲,计划将这50台电器调配给下属的甲、乙两个商店销售,其中40台给甲商店,10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表:电视机
电饭煲
甲商店/元
100
60
乙商店/元
80
50
(1)、设集团调配给甲商店x台电视机,则调配给甲商店电饭煲台,调配给乙商店电视机台、电饭煲台;(2)、求出x的取值范围;(3)、如果阳光集团卖出这50台电器想要获得的总利润为3650元,请求出x的值.26. 如图所示,直线AB、CD相交于点O,OM⊥AB.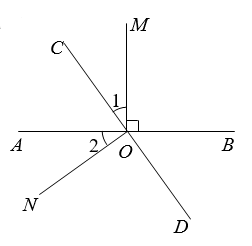 (1)、若∠1=∠2,判断ON与CD的位置关系,并说明理由;(2)、若∠1= ∠BOC,求∠MOD的度数.27. 已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.
(1)、若∠1=∠2,判断ON与CD的位置关系,并说明理由;(2)、若∠1= ∠BOC,求∠MOD的度数.27. 已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.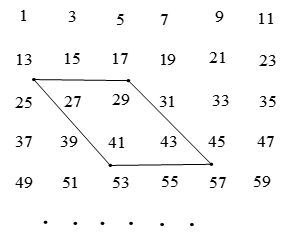 (1)、若设框住四个数中左上角的数为n,则这四个数的和为(用n的代数式表示);(2)、平行移动四边形框,若框住四个数的和为228,求出这4个数;(3)、平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.28. 如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒).
(1)、若设框住四个数中左上角的数为n,则这四个数的和为(用n的代数式表示);(2)、平行移动四边形框,若框住四个数的和为228,求出这4个数;(3)、平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.28. 如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒). (1)、当t=8时,∠AOB=°;(2)、在旋转过程中,当∠AOB=36°时,求t的值.(3)、在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.
(1)、当t=8时,∠AOB=°;(2)、在旋转过程中,当∠AOB=36°时,求t的值.(3)、在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.