浙江省宁波市北仑区2020届九年级上学期数学期末考试试卷
试卷更新日期：2020-02-04 类型：期末考试
一、选择题(每小题4分，共48分)
-
1. 下列事件是必然事件的是（ ）A、明天太阳从西方升起 B、打开电视机，正在播放广告 C、掷一枚硬币，正面朝上 D、任意一个三角形，它的内角和等于180°2. 已知 ，则 等于（ ）A、 B、 C、2 D、33. 二次函数y= x2-1的图象的顶点坐标为（ ）A、(0，0) B、(0，-1) C、( ，-1) D、( ，1)4. 如图，在Rt△ABC中，∠C=90°，AC=4，AB=5，则sinB的值是（ ）
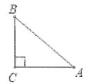A、 B、 C、 D、5. 如图，点A，B，C在⊙O上，∠A=72°，则∠OBC的度数是（ ）
A、12° B、15° C、18° D、20°6. 如图，△ABC中∠A=60°，AB=4，AC=6，将△ABC沿图示中的虚线剪开，剪下的三角形与△ABC不相似的是（ ）A、
B、
C、
D、
7. 将抛物线y=x2-2向右平移3个单位长度，再向上平移2个单位长度，则所得抛物线的解析式为（ ）A、y=(x-3)2 B、y=(x+3)2 C、y=(x+2)2+1 D、y=(x-2)28. 如图，在△ABC中，D，E分别在AB，AC上，且DE∥BC，AD=2DB，若S△ADE=3，则S四边形DBCE=（ ）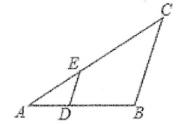
A、12 B、15 C、24 D、279. 下列四个结论，不正确的是（ ）①过三点可以作一个圆； ②圆内接四边形对角相等
③平分弦的直径垂直于弦；④相等的圆周角所对的弧也相等
A、②③ B、①③④ C、①②④ D、①②③④10. 如图，△ABC是一张周长为18cm的三角形纸片，BC=5cm，⊙O是它的内切圆，小明用剪刀在⊙O的右侧沿着与⊙O相切的任意一条直线MN剪下△AMN，则剪下的三角形的周长为（ ）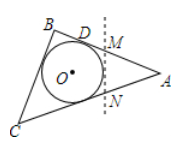
A、13cm B、8cm C、6.5cm D、随直线MN的变化而变化11. 已知二次函数y=ax2+bx+3自变量x的部分取值和对应函数值y如表：x
…
-2
-1
0
1
2
3
…
y
…
-5
0
3
4
3
0
…
则在实数范围内能使得y+5>0成立的x取值范围是（ ）
A、x>-2 B、x<-2 C、-2<x<4 D、x>-2或x<412. 如图，在菱形ABCD中，∠BAD=120°，AB=2，点E是AB边上的动点，过点B作直线CE的垂线，垂足为F，当点E从点A运动到点B时，点F的运动路径长为（ ）
A、 B、 C、2 D、二、填空题(每小题4分，共24分)
-
13. 已知线段a=4，b=9，线段c是a，b的比例中项，则线段c=。14. 一个密码箱的密码，每个数位上的数都是从0到9的自然数，若要使一次拨对的概率小于 ，则密码的位数至少要设置位．15. 已知函数y=kx2-2x+1的图象与x轴只有一个有交点，则k的值为。16. 如图，在圆O中，弦AB=4，点C在AB上移动，连接OC，过点C做CD⊥OC交圆O于点D，则CD的最大值为。
17. 如图，分别以正五边形 ABCDE的顶点A，D为圆心，以AB长为半径作 ， ，若AB=1，则阴影部分图形的周长是 。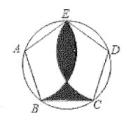
18. 如图，四边形ABCD中，∠BAD=∠BCD=90°，∠B=45°，DE⊥AC于E交AB于F，若BC=2CD，AE=2，则线段BF=。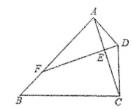
三、解答题(本大题有8小题，共78分)
-
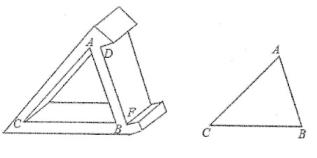
19. “马拉松竞赛”的个人竞赛项目共有三项：A．“马拉松”B．“半程马拉松”C．“迷你马拉松”。小明和小刚参加了该赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组。(1)、小明被分配到“迷你马拉松”项目组的概率为。(2)、请用画树状图或列表的方法，求出小明和小刚被分配到同一项目组的概率。20. 计算：6tan30°+cos245°-sin60°21. 在全校的科技制作大赛中，小明用木板制作了一个带有卡槽的三角形手机架。如图所示，卡槽的宽度DF与内三角形ABC的AB边长相等．已知AC=20cm，BC=18cm，∠ACB=50°，某款手机的最长边为17cm，小明能否将此手机立放入卡槽内?请说明你的理由(参考数sin50°≈0.8，cos50°≈0.6，tan50°≈1.2)
22. 如图，下列网格由小正方形组成，点A，B，C都在正方形网格的格点上。(1)、在图1中画出一个以线段BC为边，且与△ABC面积相等但不全等的格点三角形；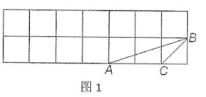
(2)、在图2和图3中分别画出一个以线段AB为边，且与△ABC相似(但不全等)的格点三角形，并写出所画三角形与△ABC的相似比。（相同的相似比算一种）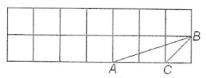
图2，相似比k=
图3，相似比k=
23. 如图，已知在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D，以AB上点O为圆心作⊙O，使⊙O经过点A和点D。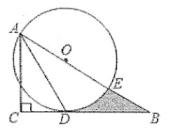
(1)、判断直线BC与⊙O的位置关系，并说明理由；(2)、若AE=6，劣弧DE的长为π，求线段BD，BE与劣弧DE所围成的阴影部分的面积(结果保留根号和π)24. 网络销售是一种重要的销售方式。某农贸公司新开设了一家网店，销售当地农产品，其中一种当地特产在网上试销售，其成本为每千克2元．公司在试销售期间，调查发现，每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中2<x≤10)
(1)、若5<x≤10，求y与x之间的函数关系式；(2)、销售单价x为多少元时，每天的销售利润最大?最大利润是多少元?25. 如图，已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1，且抛物线经过B(1，0)，C(0，3)两点，与x轴交于点A
(1)、求抛物线的解析式；(2)、如图1，在抛物线的对称轴直线x=-1上找一点M，使点M到点B的距离与到点C的距离之和最小，求出点M的坐标；(3)、如图2，点Q为直线AC上方抛物线上一点，若∠CBQ=45°，请求出点Q坐标26. 等腰△ABC中，AB=AC，作△ABC的外接圆⊙O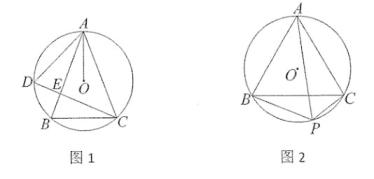
(1)、如图1，点D为 上一点(不与A，B重合)，连接AD，CD，A0，记CD与AB的交点为E。①设∠BAD=x，∠OAC=y，若∠ABC+∠DCB=n，请用含n与x的式子表示y
②当AB⊥CD时，若AO=3，AC=4 ，求AD的长；
(2)、如图2，点P为 上一点(不与B，C重合)，当BC=AB，AP=8时，设S=S△BPC+ S△ABP ， 求BP为何值时，S有最大值?并请直接写出此时⊙O的半径。