浙江省长兴县2019-2020学年七年级上学期数学期末考试试卷

试卷更新日期：2020-02-04 类型：期末考试

进入出卷网下载

一、选择题(本题有10小题，每小题3分，共30分)

1. 2020的相反数是（）

A、 -2020 B、2020 C、 $- \frac{1}{2020}$ D、 $\frac{1}{2020}$

查看试题解析
2. 2019年天猫双十一交易额最终定格在2684亿元，再次刷新双十一交易额记录，则2684亿元用科学记数法表示为（）

A、2684×10³元 B、26.84×10¹⁰元 C、0.2684×10¹²元 D、2.684×10¹¹元

查看试题解析
3. 已知∠1与∠2互补，∠1=54°，则∠2为（）

A、54° B、36° C、126° D、136°

查看试题解析
4. 下列说法正确的是（）

A、 $- \frac{3 x y}{5}$ 的系数是3 B、2m²n的次数是2次 C、 $\frac{x - 2 y}{3}$ 是多项式 D、x²-x-1的常数项是1

查看试题解析
5. 一个正数的两个平方根分别是2a-1与-a+2，则a的值为（）

A、1 B、-2 C、2 D、-1

查看试题解析
6. 把方程 $\frac{x - 1}{0.6} - \frac{0.5 x + 8}{0.9} = 16$ 的分母化为整数，结果应为（）

A、 $\frac{x - 1}{6} - \frac{5 x + 8}{9} = 16$ B、 $\frac{10 x - 10}{6} - \frac{5 x + 8}{9} = 16$ C、 $\frac{10 x - 10}{6} - \frac{5 x + 80}{9} = 160$ D、 $\frac{x - 1}{6} - \frac{5 x + 8}{9} = 160$

查看试题解析
7. 如果代数式x²+2x的值为5，那么代数式2x²+4x-3的值等于（）

A、2 B、5 C、7 D、13

查看试题解析
8. 若实数a，b，c在数轴上对应点的位置如图所示，则|a+b|+|a+c|-|b-c|可化简为（）

A、0 B、2a+2b C、2b-2c D、2a+2

查看试题解析
9. 某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为了使每天生产的螺钉和螺母刚好配套，设安排x名工人生产螺钉，则下面所列方程正确的是（）

A、2×1000(26-x)=800x B、1000(26-x)=2×800x C、1000(13-x)=800x D、1000(26-x)=800x

查看试题解析
10. 甲、乙两名运动员在圆形跑道上从A点同时出发，并按相反方向匀速跑步，甲的速度为每秒6米，乙的速度为每秒7米，当他们第一次在A点再度相遇时跑步就结束．则从他们开始出发(算第一次相遇)到结束(算最后一次相遇)共相遇次数是（）

A、13 B、14 C、42 D、43

查看试题解析

二、填空题(本题有6小题，每小题2分，共12分)

11. 我国在数的发展史上有辉煌的成就，早在东汉初，我国著名的数学著作《九章算术》明确提出了“正负术”．如果“盈5”记为“+5”，那么“亏7”可以记为。

查看试题解析
12. 计算： ${}^{3}{\sqrt{- 27}}$ =。

查看试题解析
13. 如图，已知点O是直线AB上一点，∠1=40°，射线OD平分∠BOC，则∠2的度数是。

查看试题解析
14. 若3x^m+5y²与x²yⁿ的和仍为单项式，则mⁿ=。

查看试题解析
15. 若关于x的方程 $x - \frac{4 - a x}{6} = \frac{x + 4}{6} - 1$ 的解是正整数，则符合条件的所有整数a的和是。

查看试题解析
16. 如图，射线OC平分角形纸片的∠AOB，若把∠AOB沿射线OC对折成∠COB(OA与OB重合)，从点O引一条射线OE，使∠BOE= $\frac{1}{2}$ ∠EOC，再沿射线OE把角剪开，若把纸片展开后得到的3个角中最大的一个角为76°，则∠AOB= 。

查看试题解析

三、解答题(共58分)

17. 计算：

(1)、12-8÷(-2)

(2)、-2³+ ${}^{3}{\sqrt{- 8}}$ ÷(-8)× $\sqrt{64}$

查看试题解析
18. 如图，平面内有三个点A，B，C，请你根据下列要求完成作图(作图工具不限)

①画直线AB，射线CB，线段AC；
②过点C作直线l⊥直线AB，垂足为D。

查看试题解析
19. 化简并求值：2（3a²b-ab³)-3(2a²b-ab) 其中a= $\frac{1}{2}$ ， b=-4

查看试题解析
20. 如图，已知点C为线段AB上一点，AC=15cm，CB= $\frac{3}{5}$ AC，点D，E分别为线段AC，AB的中点，求线段AB与DE的长。

查看试题解析
21. 如图，现有5张写着不同数的卡片，请按要求完成下列问题：

(1)、从中任选2张卡片，使这2张卡片上的数的乘积最大，则该乘积的最大值是多少?

(2)、从中任选4张卡片，用卡片上的数和加、减、乘、除四则运算(可用括号，每个数都要用且只能用一次)列出两个不同的算式(每个算式可选用不同的卡片)，使其计算结果为24。

查看试题解析
22. 如图，已知直线AB，CD相交于点O，∠COE=90°

(1)、若∠AOC=36°，求∠BOE的度数；

(2)、若∠BOD：∠BOC=2：7，求∠AOE的度数。

查看试题解析
23. 目前节能灯在各地区基本已普及使用，某市一商场为响应号召推广销售，该商场计划用3800元购进两种节能灯共120只，这两种节能灯的进价、售价如下表：

型号

进价(元/只)

售价(元/只)

甲型

20

26

乙型

48

60

(1)、则甲、乙两种型号节能灯各进多少只?

(2)、全部售完这120只节能灯后，该商场获利多少元?

查看试题解析
24. 如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示-12，点B表示10，点C表示20，我们称点A和点C在数轴上相距32个长度单位．动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半，之后立刻恢复原速；同时，动点Q从点C出发，以1单位/秒的速度沿着折线数轴的负方向运动，从点B运动到点O期间速度变为原来的两倍，之后也立刻恢复原速．设运动的时间为t秒。则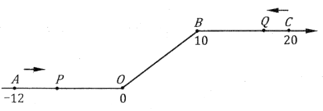

(1)、动点P从点A运动至点C需要时间多少秒?

(2)、若P，Q两点在点M处相遇，则点M在折线数轴上所表示的数是多少?

(3)、求当t为何值时，P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等。

查看试题解析

型号	进价(元/只)	售价(元/只)
甲型	20	26
乙型	48	60