浙江省长兴县2020届九年级上学期数学期末考试试卷
试卷更新日期：2020-02-04 类型：期末考试
一、选择题(本题有10小题，每小题3分，共30分)
-
1. 已知 ，则代数式 的值为（ ）A、 B、 C、 D、2. 下列事件是必然事件的是（ ）A、打开电视机，正在播放动画片 B、经过有交通信号灯的路口，遇到红灯 C、过三点画一个圆 D、任意画一个三角形，其内角和是180°3. 若扇形的圆心角为90°，半径为6，则该扇形的弧长为（ ）A、 B、 C、 D、4. 在△ABC中，∠C=90°，AC=4，BC=3，则sinA的值是（ ）A、 B、 C、 D、5. 如图，已知正五边形 ABCDE内接于⊙O，连结BD，则∠ABD的度数是（ ）
A、60° B、70° C、72° D、144°6. 将抛物线y=-x2向右平移3个单位后，得到的抛物线的解析式是（ ）A、y=-(x+3)2 B、y=-(x-3)2 C、y=-x2+3 D、y=-x2-37. 如图，在△ABC中，DE∥BC， = ，BC=12，则DE的长是（ ）
A、3 B、4 C、5 D、68. 如图，AC是⊙O的直径，弦BD⊥AO于点E，连结BC，过点O作OF⊥BC于点F，若BD=8cm，AE=2cm，则OF的长度是（ ）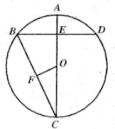
A、 cm B、 cm C、2.5cm D、3cm9. 如图，四边形ABCD内接于⊙O，AB为直径，AD=CD，过点D作DE⊥AB于点E，连结AC交DE于点F若sin∠CAB= ，DF=5，则BC的长为（ ）
A、8 B、10 C、12 D、1610. 如图，抛物线y=x2+2x与直线y= x+1交于A，B两点，与直线x=2交于点D将抛物线沿着射线AB方向平移2 个单位在整个平移过程中，点D经过的路程为（ ）
A、 B、 C、 D、6二、填空题(本题有6小题，每小题4分，共24分)
-
11. 二次函数y=(x-2)2+1图象的对称轴是。12. 已知线段c是线段a、b的比例中项，且a=4，b=9，则线段c的长度为 。
13. 一个不透明的盒子里有若干个除颜色外其他完全相同的小球，其中有9个黄球，每次摸球前先将盒子里的球摇匀任意摸出一个球记下颜色后再放回盒子，通过大量重复摸球实验后发现，摸到黄球的频率稳定在30%，那么估计盒子中小球的个数为 。14. 如图，AB是⊙O的直径，点C和点D是⊙O上位于直径AB两侧的点，连结AC，AD，BD，CD，若⊙O的半径是5，BD=8，则sin∠ACD的值是。
15. 如图，在Rt△ABC中，∠C=90°，AC=8，点D在边BC上，CD=6，BD=10．点P是线段AD上一动点当半径为4的⊙P与△ABC的一边相切时，AP的长为。
16. 如图，在平面直角坐标系中抛物线y=x2-3x+2与x轴交于A、B两点，与y轴交于点C，D是对称轴右侧抛物线上一点，且tan∠DCB=3，则点D的坐标为。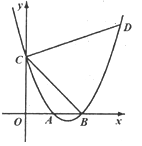
三、解答题(本题共有8小题，共66分)
-
17. 计算：18. 如图，AC、BD交于点E，BC=CD，且BD平分∠ABC。
(1)、求证：△AEB∽△CED。(2)、若BC=6，EC=3，AE=2，求AB的长。19. 在一个不透明的盒子中装有5张卡片，5张卡片的正面分别标有数字1，2，3，4，5，这些卡片除数字外，其余都相同。(1)、从盒子中任意抽取一张卡片，恰好抽到标有偶数的卡片的概率是多少?(2)、先从盒子中任意抽取一张卡片，再从余下的4张卡片中任意抽取一张卡片，求抽取的2张卡片上标有的数字之和大于5的概率画树状图或列表求解)20. 如果一条抛物线y=ax2+bxc(a≠0)与坐标轴有三个交点那么以这三个交点为顶点的三角形称为这条抛物线的“抛物线三角形”(1)、命题“任意抛物线都有抛物线三角形”是（填“真”或“假”）命题；(2)、若抛物线解析式为y=x2-4x+3，求其“抛物线三角形”的面积。
21. 如图是某学校体育看台侧面的示意图，看台AC的坡比i为1：2，看 高度BC为12米，从顶棚的D处看E处的仰角a=18°，CD距离为5米，E处到观众区底端A处的水平距离AF为3米。(sin18°≈0.31，tan18°≈0.32，结果精确到0.1米)
(1)、求AB的长；(2)、求EF的长。22. 如图，某农场准备围建一个中间隔有一道篱笆的矩形花圃，现有长为18米的篱笆，边靠墙，若墙长a=6米，设花圃的一边AB为x米；面积为S米2。
(1)、求S与x的函数关系式及x值的取值范围；(2)、若边BC不小于3米，这个花圃的面积有最大值和最小值吗?如果有，求出最大值和最小值；如果没有，请说明理由。23. 如图，四边形ABCE内接于⊙O，AB是⊙O的直径，点D在AB的延长线上，延长AE交BC的延长线于点F，点C是BF的中点，∠BCD=∠CAE
(1)、求证：CD是⊙O的切线；(2)、求证：△CEF是等腰三角形；(3)、若BD=1，CD=2，求 cos∠CBA的值及EF的长。24. 如图1，在平面直角坐标系中抛物线y= x2+bx+c与x轴交于A、B两点，与y轴交于点C已知BC=
，tan∠OBC= 
(1)、求抛物线的解析式；(2)、如图2，若点P是直线BC上方的抛物线上一动点，过点P作y轴的平行线交直线BC于点D，作PE⊥BC于点E，当点P的横坐标为2时，求△PDE的面积；(3)、若点M为抛物线上的一个动点，以点M为圆心， 为半径作⊙M，当⊙M在运动过程中与直线BC相切时，求点M的坐标(请直接写出答案)