浙江省湖州市长兴县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-04 类型:期末考试
一、选择题(本题有10小题,每小题3分,共30分)
-
1. 点(-1,2)关于x轴的对称点坐标是( )A、(2,-1) B、(-1,-2) C、(1,2) D、(1,-2)2. 若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( )A、1 B、2 C、3 D、83. 不等式1+x≥2-3x的解是( )
A、x≥ B、x≥ C、x≤ D、x≤4. 下列四个图形中,线段BE是△ABC的高的是( )A、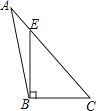 B、
B、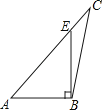 C、
C、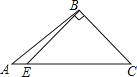 D、
D、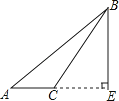 5. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
5. 如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( ) A、∠A=∠D B、AC=DF C、AB=ED D、BF=EC6. 点P是直线y=-x+ 上一动点,O为原点,则OP的最小值为( )A、2 B、 C、1 D、7. 如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( )
A、∠A=∠D B、AC=DF C、AB=ED D、BF=EC6. 点P是直线y=-x+ 上一动点,O为原点,则OP的最小值为( )A、2 B、 C、1 D、7. 如图,BD是△ABC的角平分线,AE⊥BD,垂足为F.若∠ABC=35°,∠C=50°,则∠CDE的度数为( ) A、35° B、40° C、45° D、50°8. 若关于x的不等式组 的解为x>a,则a的取值范围是( )A、a>2 B、a≥2 C、a<2 D、a≤29. 某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断错误的是( )
A、35° B、40° C、45° D、50°8. 若关于x的不等式组 的解为x>a,则a的取值范围是( )A、a>2 B、a≥2 C、a<2 D、a≤29. 某通讯公司就上宽带网推出A,B,C三种月收费方式.这三种收费方式每月所需的费用y(元)与上网时间x(h)的函数关系如图所示,则下列判断错误的是( )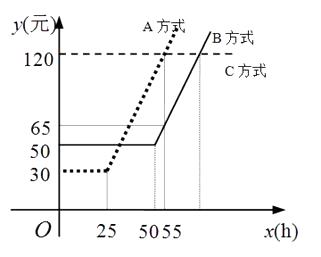 A、每月上网时间不足25 h时,选择A方式最省钱 B、每月上网费用为60元时,B方式可上网的时间比A方式多 C、每月上网时间为35h时,选择B方式最省钱 D、每月上网时间超过70h时,选择C方式最省钱10. 如图,在等边△ABC中,AB=15,BD=6,BE=3,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )
A、每月上网时间不足25 h时,选择A方式最省钱 B、每月上网费用为60元时,B方式可上网的时间比A方式多 C、每月上网时间为35h时,选择B方式最省钱 D、每月上网时间超过70h时,选择C方式最省钱10. 如图,在等边△ABC中,AB=15,BD=6,BE=3,点P从点E出发沿EA方向运动,连结PD,以PD为边,在PD右侧按如图方式作等边△DPF,当点P从点E运动到点A时,点F运动的路径长是( )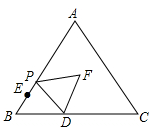 A、8 B、10 C、 D、12
A、8 B、10 C、 D、12二、填空题(本题有6小题,每小题4分,共24分)
-
11. 点(2,-1)所在的象限是第象限。12. 命题“三角形的三个内角中至少有两个锐角”是(填“真命题”或“假命题”).13. “x的 与x的和不超过5”用不等式表示为。14. 如图,在△ABC中,AB=AC,∠ACD=110°,则∠A=度。
 15. 如图,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若点B(m,3),C(n,-5),A(4,0),则AD·BC=。
15. 如图,直线BC经过原点O,点A在x轴上,AD⊥BC于D,若点B(m,3),C(n,-5),A(4,0),则AD·BC=。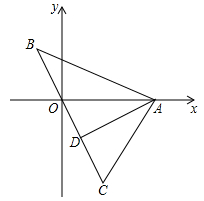 16. 如图,△AOB中,∠AOB=90°,OA=OB,等腰直角△CDF的直角顶点C在边OA上,点D在边OB上,点F在边AB上,如果△CDF的面积是△AOB的面积的 ,OD=2,则△AOB的面积为。
16. 如图,△AOB中,∠AOB=90°,OA=OB,等腰直角△CDF的直角顶点C在边OA上,点D在边OB上,点F在边AB上,如果△CDF的面积是△AOB的面积的 ,OD=2,则△AOB的面积为。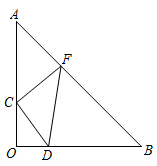
三、解答题(本题共有8小题,共66分)
-
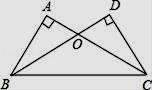
17. 解不等式组:18. 如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.
 19. 一次函数的图象过M(6,-1),N(-4,9)两点。(1)、求函数的表达式。(2)、当y<1时,求自变量x的取值范围。20. 如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点在网格线的交点的三角形)ABC的顶点A,C坐标分别是(a,5),(-1,b)。
19. 一次函数的图象过M(6,-1),N(-4,9)两点。(1)、求函数的表达式。(2)、当y<1时,求自变量x的取值范围。20. 如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点在网格线的交点的三角形)ABC的顶点A,C坐标分别是(a,5),(-1,b)。 (1)、求a,b的值;(2)、①在图中作出直角坐标系;
(1)、求a,b的值;(2)、①在图中作出直角坐标系;②在图中作出△ABC关于y轴对称的图形△A′B′C′。
21. 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD。 (1)、求证:△BCE≌△DCF(2)、若AB=21,AD=9,BC=CD=10,求AC的长。22. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲,乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示。
(1)、求证:△BCE≌△DCF(2)、若AB=21,AD=9,BC=CD=10,求AC的长。22. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲,乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示。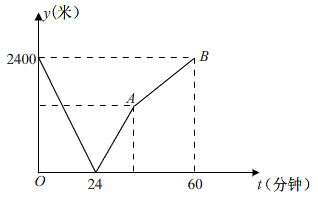 (1)、根据图象信息,当t=分钟时甲乙两人相遇,甲的速度为米/分钟。(2)、求线段AB所表示的函数表达式。23. 如图
(1)、根据图象信息,当t=分钟时甲乙两人相遇,甲的速度为米/分钟。(2)、求线段AB所表示的函数表达式。23. 如图 (1)、一节数学课上,老师提出了这样一个问题:如图1,点P是等腰Rt△ABC内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?
(1)、一节数学课上,老师提出了这样一个问题:如图1,点P是等腰Rt△ABC内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?小明通过观察,分析,思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连结P′P,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP′B,连结P′P,求出∠APB的度数。
请参考小明的思路,任选一种写出完整的解答过程。
(2)、【类比探究】如图,若点M是等腰Rt△ABC外一点,MA=3,MB=1,MC= ,请直接写出∠AMB的度数。24. 如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(-1,a),l1与y轴交于点C,l2与x轴交于点A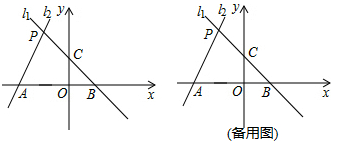 (1)、求a的值及直线l1的解析式。(2)、求四边形PAOC的面积。(3)、在x轴上方有一动直线平行于x轴,分别与l1 , l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由。
(1)、求a的值及直线l1的解析式。(2)、求四边形PAOC的面积。(3)、在x轴上方有一动直线平行于x轴,分别与l1 , l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由。