浙江省温州市苍南县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期：2020-02-04 类型：期末考试
一、选择题(本题有10小题，每小题3分，共30分．)
-
1. 下列长度的三条线段能组成三角形的是（ ）A、1cm， 1cm， 3cm B、1cm 2cm． 3cm C、1cm， 2cm， 2cm D、1cm， 4cm， 2cm2. 在直角坐标系中，点(-1，2)位于（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 在直角坐标系中，已知点(2，b)在直线y=2x上，则b的值为（ ）A、1 B、-1 C、4 D、-44. 对不等式a>b进行变形，结果正确的是（ ）A、a-b<0 B、a-2>b-2 C、2a<2b D、1-a>1-b5. 如图，DE⊥AC于点E，BF⊥AC于点F，且DE=BF，若利用“HL”证明△DEC≌△BFA，则需添加的条件是（ ）
A、DC=BA B、EC=FA C、∠D=∠B D、∠DCE=BAF6. 下列选项中，可以用来证明命题“若|a|>2，则a>2”是假命题的反例的是（ ）A、a=3 B、a=0 C、a=-2 D、a=-37. 如图，在边长为4的等边三角形ABC中，点D，E分别是边BC，AC的中点，DF⊥AB于点F，连结EF，则EF的长为（ ）
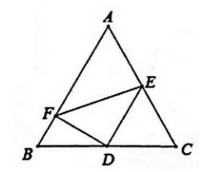A、 B、2.5 C、 D、38. 已知点A(x1 ， a)，B(x1+1，b)都在函数y=-2x+3的图象上，下列对于a，b的关系判断正确的是（ ）A、a-b=2 B、a-b=-2 C、a+b=2 D、a+b=-29. 如图，在△ABC中，点D是BC边上任一点，点F，G，E分别是AD，BF，CF的中点，连结GE，若△FGE的面积为8，则△ABC的面积为（ ）
A、32 B、48 C、64 D、7210. 直角坐标系中，我们定义横、纵坐标均为整数的点为整点在0<x<3内，直线y=x+2和y=-x所围成的区域中，整点一共有（ ）A、8个 B、7个 C、6个 D、5个二、填空题(本题有8小题，每小题3分，共24分)
-
11. 函数y= 中，自变量x的取值范围是。12. “x的3倍减去y的差是正数”用不等式表示为 。13. 点M(3，-2)关于x轴的对称点M1的坐标是。14. 如图，Rt△ABC中，∠ACB=90°，∠A=28°，D是AB的中点，则∠DCB=度。
15. 如图，在△ABC中，AB=AC，∠BAC=50°，D是边BC的中点，DE垂直AC于点E，则∠EDC=度。
16. 如图，直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m，3)，则方程组 的解为。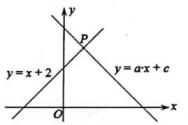
17. 如图，BD是△ABC的角平分线，AE⊥BD，垂足为F，且交线段BC于点E，连结DE，若∠C=50°，设∠ABC=x°，∠CDE=y°，则y关于x的函数表达式为。
18. 如图，在直角坐标系中，点A(0，4)，B(-3，0)，C是线段AB的中点，D为x轴上一个动点，以AD为直角边作等腰直角△ADE(点A，D，E以顺时针方向排列)，其中∠DAE=90°，则点E的横坐标等于 ， 连结CE，当CE达到最小值时，DE的长为。
三、解答题(本题有6小题，共46分)
-
19. 解不等式组 并把它的解集在数轴上表示出来。
20. 在4×4的正方形网格中建立如图1、2所示的直角坐标系，其中格点A，B的坐标分别是(0，1)，(-1，-1)。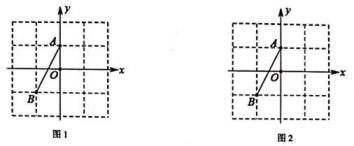
(1)、请图1中添加一个格点C，使得△ABC是轴对称图形，且对称轴经过点(0，-1)。(2)、请图2中添加一个格点D，使得△ABD也是轴对称图形，且对称轴经过点(1，1)。21. 已知：如图，∠ACB=∠DCE，AC=BC，CD=CE，AD交BC于点F，连结BE。
(1)、求证：△ACD≌△BCE。(2)、延长AD交BE于点H，若∠ACB=30°，求∠BHF的度数。22. 如图，直角坐标系中，点C是直线y= x上第一象限内的点点A(1，0)，以AC为边作等腰Rt△ACB，AC=BC点B在x轴上，且位于点A的右边，直线BC交y轴于点D。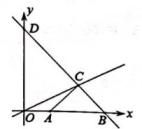
(1)、求点B，C的坐标；(2)、点A向上平移m个单位落在△OCD的内部(不包括边界)，求m的取值范围。23. “垃圾分类”意识已经深入人心．我校王老师准备用2000元(全部用完)购买A，B两类垃圾桶，已知A类桶单价20元，B类桶单价40元，设购入A类桶x个，B类桶y个。(1)、求y关于x的函数表达式。(2)、若购进的A类桶不少于B类桶的2倍。①求至少购进A类桶多少个?
②根据临场实际购买情况，王老师在总费用不变的情况下把一部分A类桶调换成另一种C类桶，且调换后C类桶的数量不少于B类桶的数量，已知C类桶单价30元，则按这样的购买方式，B类桶最多可买个。(直接写出答案)24. 如图，直角坐标系中，直线y=kx+b分别与x轴、y轴交于点A(3，0)，点B(0，-4)，过D(0，8)作平行x轴的直线CD，交AB于点C，点E(0，m)在线段OD上，延长CE交x轴于点F，点G在x轴正半轴上，且AG=AF。
(1)、求直线AB的函数表达式。(2)、当点E恰好是OD中点时，求△ACG的面积。(3)、是否存在m，使得△FCG是直角三角形?若存在，直接写出m的值；若不存在，请说明理由。