浙江省杭州市监安市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-04 类型:期末考试
一、选择题:本大题有10个小题,每小题3分,共30分.
-
1. 若点A(-2,4)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若长度分别为a,3,5的三条线段能组成一个三角形,则下列选项中符合条件的a值是( )A、1 B、2 C、3 D、93. 在 ,-2,1,-3四个数中,满足不等式x<-2的有( )A、1个 B、2个 C、3个 D、4个4. 如果一次函数y=kx+b的图象经过第二第四象限,且与x轴正半轴相交,那么( )A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<05. 已知△ABC≌△A1B1C1 , A和A1对应,B和B1对应,∠A=70°,∠B1=50°,则∠C的度数为( )A、70° B、50° C、120° D、60°6. 已知(-2,y1),(-1,y2),(1.7,y3)是直线y=-5x+b(b为常数)上的三个点,则y1 , y2,y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y1>y3>y2 D、y3>y1>y27. 如图,△ABC中,AB=AC,∠BAC=100°,DE是AC边的垂直平分线,则∠BAE的度数为( )
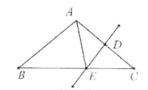 A、60° B、50° C、45° D、40°8. 已知x>y,则下列不等式成立的是( )A、-2x>-2y B、4x>3y C、5-x>5-y D、x-2>y-39. 如图,在4×4方格中,以AB为边,第三个顶点也在格点上的等腰三角形可以作出( )
A、60° B、50° C、45° D、40°8. 已知x>y,则下列不等式成立的是( )A、-2x>-2y B、4x>3y C、5-x>5-y D、x-2>y-39. 如图,在4×4方格中,以AB为边,第三个顶点也在格点上的等腰三角形可以作出( ) A、7个 B、6个 C、4个 D、3个10. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中①AC=BD;②∠AMB=30°;③ △OME≌△OFM或△OMC≌△OFM :④MO平分∠BMC.正确的个数有( )
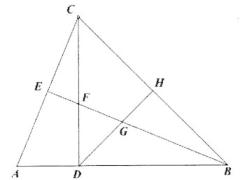
A、7个 B、6个 C、4个 D、3个10. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=30°,连接AC,BD交于点M,AC与OD相交于E,BD与OA相交于F,连接OM.则下列结论中①AC=BD;②∠AMB=30°;③ △OME≌△OFM或△OMC≌△OFM :④MO平分∠BMC.正确的个数有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题:本大题有6个小题,每小题4分,共24分。
-
11. x减去y大于-4,用不等式表示为 。12. 若点M(a-3,a+4)在x轴上,则点M的坐标是。13. 在△ABC中,∠A:∠B:∠C=2:3:4,则∠C的度数是。14. 已知直角三角形的两条边长分别是3和5,则第三条边的长是 。15. 某商店卖水果,数量x(千克)与售价y(元)之间的关系如下表,(y是x的次函数):
x/千克
0.5
1
1.5
2
…
y/元
1.6+0.1
3.2+0.1
4.8+0.1
6.4+0.1
当x=7千克时,售价y=元。
16. 如图,CD是△ABC的角平分线,AE⊥CD于E,BC=6,AC=4,△ABC的面积是9,则△AEC的面积是。
三、解答题:本大题有7个小题.共66分.
-
17. 解下列不等式(组):(1)、4x-1<2x-3(2)、18. 如图所示,△ABC在正方形网格中,若点A的坐标是(2,4),点B的坐标是(-1,0),按要求解答下列问题:
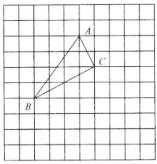
①在图中建立正确的平面直角坐标系,写出点C的坐标。
②在图中作出△ABC关于x轴对称的△A1B1C1。
19. 如图,已知B,D,E,C在同一直线上,DC=BE,∠ADE=∠AED。求证:AB=AC。 20. 如图1,公路上有A,B,C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图2所示。
20. 如图1,公路上有A,B,C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图2所示。
 (1)、求y与x之间的函数关系式及自变量的取值范围。(2)、汽车距离C站20千米时已行驶了多少时间?21. 如图,在△ABC中,AC<AB<BC,AD是高线,∠B=α,∠C=β。
(1)、求y与x之间的函数关系式及自变量的取值范围。(2)、汽车距离C站20千米时已行驶了多少时间?21. 如图,在△ABC中,AC<AB<BC,AD是高线,∠B=α,∠C=β。 (1)、用直尺与圆规作三角形内角∠BAC的平分线AE(不写作法,保留作图痕迹)。(2)、在(1)的前提下,判断①∠EAD= ,②∠EAD= 中哪一个正确?并说明理由。
(1)、用直尺与圆规作三角形内角∠BAC的平分线AE(不写作法,保留作图痕迹)。(2)、在(1)的前提下,判断①∠EAD= ,②∠EAD= 中哪一个正确?并说明理由。