浙江省宁波市鄞州区2020届九年级上学期数学期末考试试卷
试卷更新日期：2020-02-04 类型：期末考试
一、选择题(每小题4分，共48分)
-
1. 抛物线y=2x2的开口方向是（ ）A、向下 B、向上 C、向左 D、向右2. 已知2x=5y(y≠0)，则下列比例式成立的是（ ）A、 B、 C、 D、3. 将抛物线y=x2向上平移3个单位后得到的抛物线的函数表达式是（ ）A、y=x2+3 B、y=x2-3 C、y=(x+3)2 D、y=(x-3)24. 下列事件中，是必然事件的是（ ）A、抛掷一枚硬币正面向上 B、从一副完整扑克牌中任抽一张，恰好抽到红桃A C、今天太阳从西边升起 D、从4件红衣服和2件黑衣服中任抽3件有红衣服5. 如果两个相似多边形的面积之比为1：4，那么它们的周长之比是( ）
A、1：2 B、1：4 C、1：8 D、1：166. 圆内接正六边形的边长为3，则该圆的直径长为（ ）A、3 B、3 C、3 D、67. 对一批衬衣进行抽检，得到合格衬衣的频数表如下，若出售1200件衬衣，则其中次品的件数大约是（ ）抽取件数(件)
50
100
150
200
500
800
1000
合格频数
48
98
144
193
489
784
981
A、12 B、24 C、1188 D、11768. 如图，点A、B、C是⊙O上的点，OB∥AC，连结BC交OA于点D，若∠ADB=60°，则∠AOB的度数为（ ）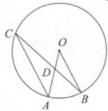
A、30° B、40° C、45° D、50°9. 如图，在△ABC中，∠C=90°，过重心G作AC、BC的垂线，垂足分别为D、E，则四边形GDCE的面积与△ABC的面积之比为（ ）
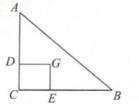A、 B、 C、 D、10. 如图，AB为⊙O的直径，点D是弧AC的中点，过点D作DE⊥AB于点E，延长DE交⊙O于点F，若AC=12，AE=3，则⊙O的直径长为（ ）
A、10 B、13 C、15 D、1611. 若A(a，b)，B(a2 ， c)两点均在函数y=(x-1)2-2019的图象上，且1≤a<2，则b与c的大小关系为（ ）
A、b<c B、b≤c C、b>c D、b≥c12. 如图，矩形ABCD∽矩形FAHG，连结BD，延长GH分别交BD、BC于点Ⅰ、J，延长CD、FG交于点E，一定能求出△BIJ面积的条件是（ ）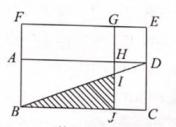
A、矩形ABJH和矩形HJCD的面积之差 B、矩形ABJH和矩形HDEG的面积之差 C、矩形ABCD和矩形AHGF的面积之差 D、矩形FBJG和矩形GJCE的面积之差二、填空题(每小题4分，共24分)
-
13. 一枚质地均匀的骰子，六个面分别标有数字1，2，3，4，5，6，抛掷一次，恰好出现“正面朝上的数字是5”的概率是。14. 在Rt△ABC中，∠C=90°，∠A=45°，AC=4，则AB的长是。15. 如图，在△ABC中，点D、E分别在AB、AC上，∠AED=∠B，若AE=2，△ADE的面积为4，四边形BCED的面积为5，则AB的长为。
16. 如图，把△ABC绕着点A顺时针方向旋转角度a(0°<a<90°)，得到△AB'C'，若B'，C，C'三点在同一条直线上，∠B'CB=46°，则a的度数是。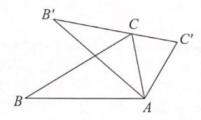
17. 如图，点B(-1，a)、C(b，-4)在⊙A上，点A在x轴的正半轴上，点D是⊙A上第象限内的一点，若∠D=45°，则圆心A的坐标为。
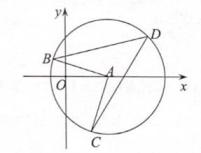18. 如图，在平面直角坐标系中，点A，B的坐标分别是A(2，2)，B(5，5)，若二次函数y=ax2+bx+c的图象过A，B两点，且该函数图象的顶点为M(x，y)，其中x，y是整数，且0<x<7，0<y<7，则a的值为。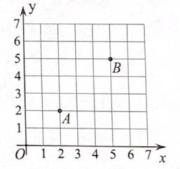
三、解答题(第19题6分，第20、21题8分，第22~24题各10分，第25题12分，第26题14分，共78分)
-
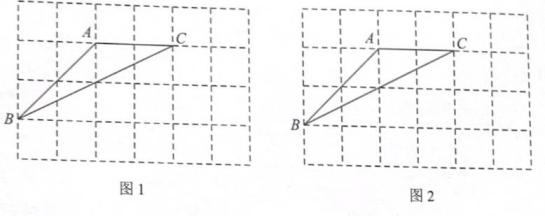
19. 计算：3tan30°＋cos245°－2sin60°．20. 如图是由24个小正方形组成的网格图，每一个正方形的顶点都称为格点，△ABC的三个顶点都是格点．请按要求完成下列作图，每个小题只需作出一个符合条件的图形。
(1)、在图1网格中找格点D，作直线AD，使直线AD平分△ABC的面积；(2)、在图2网格中找格点E，作直线AE，使直线AE把△ABC的面积分成1：2两部分21. 在一个不透明的小布袋中装有4个质地、大小完全相同的小球，它们分别标有数字0，1，2，3，小明从布袋里随机摸出一个小球，记下数字为x，小红在剩下的3个小球中随机摸出一个小球，记下数字为y，这样确定了点M的坐标(x，y)(1)、画树状图或列表，写出点M所有可能的坐标；(2)、小明和小红约定做一个游戏，其规则为：若M在第一象限，则小明胜；否则，小红胜；这个游戏公平吗?请你作出判断并说明理由。22. 如图，在电线杆上的点C处引同样长度的拉线CE，CF固定电线杆CD，在离电线杆6米处安置测角仪AB(其中点B、E、D、F在同一条直线上)，在A处测得电线杆上点C处的仰角为30°，测角仪AB的高为 米。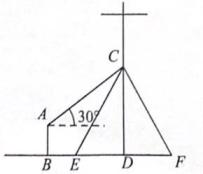
(1)、求电线杆上点C离地面的距离CD(2)、若拉线CE，CF的长度之和为18米，求固定点E和F之间的距离。23. 如图1，小明用一张边长为6cm的正方形硬纸板设计一个无盖的长方体纸盒，从四个角各剪去一个边长为xcm的正方形，再折成如图2所示的无盖纸盒，记它的容积为ycm3 ．
(1)、y关于x的函数表达式是 ， 自变量x的取值范围是。(2)、为探究y随x的变化规律，小明类比二次函数进行了如下探究①列表：请你补充表格中的数据
x
0
0.5
1
1.5
2
2.5
3
y
0
12.5
13.5
2.5
0
②描点：把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；
③连线：用光滑的曲线顺次连结各点
(3)、利用函数图象解决：若该纸盒的容积超过12cm3 ， 估计正方形边长x的取值范围．(保留一位小数)24. 已知：如图，在半圆O中，直径AB的长为6，点C是半圆上一点，过圆心O作AB的垂线交线段AC的延长线于点D，交弦BC于点E。
(1)、求证：∠D=∠ABC；(2)、记OE=x，ODy，求y关于x的函数表达式(3)、若OE=CE，求图中阴影部分的面积25. 定义：若函数y=x2+bx+c(c≠0)与x轴的交点A，B的横坐标为xA ， xB ， 与y轴交点的纵坐标为yC ， 若xA ， xB中至少存在一个值，满足xA=yC(或xB=yC)，则称该函数为友好函数如图，函数y=x2+2x-3与x轴的一个交点A的横坐标为-3，与y轴交点C的纵坐标为3，满足xA=yC ， 称y=x2+2x-3为友好函数。
(1)、判断y=x2-4x+3是否为友好函数，并说明理由；(2)、请探究友好函数y=x2+bx+c表达式中的b与c之间的关系；(3)、若y=x2+bx+c是友好函数，且∠ACB为锐角，求c的取值范围。26. 如图，在直角△ABC中，∠C=90°，AB=5，作∠ABC的平分线交AC于点D，在AB上取点O，以点O为圆心经过B、D两点画圆分别与AB、BC相交于点E、F(异于点B)．
(1)、求证：AC是⊙O的切线(2)、若点E恰好是AO的中点，求 的长(3)、若CF的长为①求⊙O的半径长
②点F关于BD轴对称后得到点F'，求△BFF'与△DEF'的面积之比