浙江省宁波市北仑区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-02-04 类型:期末考试
一、选择题(每小题4分,共48分)
-
1. 下列各点中,位于第二象限的是( )A、(4,3) B、(-3,5) C、(3,-4) D、(-4,-3)2. 如果三角形的两边长分别是4和9,那么第三边长可能是( )A、1 B、5 C、8 D、143. 把不等式2-x<1的解集在数轴上表示正确的是( )A、
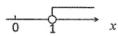 B、
B、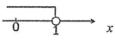 C、
C、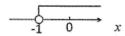 D、
D、 4. 一次函数y=5x-4的图象不经过( )A、第四象限 B、第三象限 C、第二象限 D、第一象限5. △ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题为真命题的( )A、如果∠A=2∠B=3∠C,则△ABC是直角三角形 B、如果∠A:∠B:∠C=3:4:5,则△ABC是直角三角形 C、如果a:b:c=1:2:2,则△ABC是直角三角形 D、如果a:b:c=3:4: ,则△ABC是直角三角形6. 如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
4. 一次函数y=5x-4的图象不经过( )A、第四象限 B、第三象限 C、第二象限 D、第一象限5. △ABC中∠A、∠B、∠C的对边分别是a、b、c,下列命题为真命题的( )A、如果∠A=2∠B=3∠C,则△ABC是直角三角形 B、如果∠A:∠B:∠C=3:4:5,则△ABC是直角三角形 C、如果a:b:c=1:2:2,则△ABC是直角三角形 D、如果a:b:c=3:4: ,则△ABC是直角三角形6. 如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( ) A、70° B、68° C、65° D、60°7. 如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D,则CD的长为( )
A、70° B、68° C、65° D、60°7. 如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D,则CD的长为( )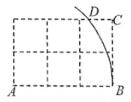 A、 B、0.8 C、 D、8. 如图,△ABC的面积为8cm2 , ∠B的平分线BP垂直AP于点P,则△PBC的面积为( )
A、 B、0.8 C、 D、8. 如图,△ABC的面积为8cm2 , ∠B的平分线BP垂直AP于点P,则△PBC的面积为( ) A、5cm2 B、4cm2 C、3cm2 D、2cm29. 如果不等式组 恰有3个整数解,则a的取值范围是( )A、a≤-1 B、a<-1 C、2<a≤-1 D、-2≤a<-110. 如图,在平面直角坐标系中,点A坐标为(2,2 ),作AB⊥x轴于点B,连接AO,将△AOB绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )
A、5cm2 B、4cm2 C、3cm2 D、2cm29. 如果不等式组 恰有3个整数解,则a的取值范围是( )A、a≤-1 B、a<-1 C、2<a≤-1 D、-2≤a<-110. 如图,在平面直角坐标系中,点A坐标为(2,2 ),作AB⊥x轴于点B,连接AO,将△AOB绕点B逆时针旋转60°得到△CBD,则点C的坐标为( )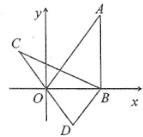 A、(-1, ) B、(-2, ) C、(- ,1) D、(- ,2)11. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图图能大致反映y与x函数关系的是( )
A、(-1, ) B、(-2, ) C、(- ,1) D、(- ,2)11. 如图,正方形ABCD的边长为4,点E是AB的中点,点P从点E出发,沿E→A→D→C移动至终点C,设P点经过的路径长为x,△CPE的面积为y,则下列图图能大致反映y与x函数关系的是( )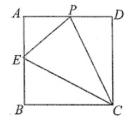 A、
A、 B、
B、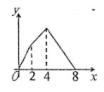 C、
C、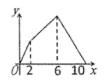 D、
D、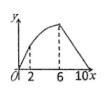 12. 如图,直线AB:y=-3x+9交y轴于A,交x轴于B,x轴上一点C(-1,0),D为y轴上一动点,把线段BD绕B点逆时针旋转90°得到线段BE,连接CE,CD,则当CE长度最小时,线段CD的长为( )
12. 如图,直线AB:y=-3x+9交y轴于A,交x轴于B,x轴上一点C(-1,0),D为y轴上一动点,把线段BD绕B点逆时针旋转90°得到线段BE,连接CE,CD,则当CE长度最小时,线段CD的长为( )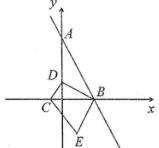 A、 B、 C、5 D、
A、 B、 C、5 D、二、填空题(每小题4分,共24分)
-
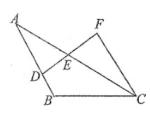
13. 已知正比例函数经过点(-1,2),该函数解析式为 。14. 若a<b,则-5a-5b(填“>”<”或“=”)15. 如图,已知AB∥CF,E为DF的中点.若AB=13cm,CF=7cm,则BD=cm。
 16. 若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n=。17. 若等腰三角形的两边长为10,6,则周长为。18. 定义:到三角形两边距离相等的点叫做三角形的准内心.已知在Rt△ABC中,∠C=90°,AC=6,BC=8,点P是△ABC的准内心(不包括顶点),且点P在△ABC的某条边上,则CP的长为。
16. 若点A(m+2,3)与点B(-4,n+5)关于y轴对称,则m+n=。17. 若等腰三角形的两边长为10,6,则周长为。18. 定义:到三角形两边距离相等的点叫做三角形的准内心.已知在Rt△ABC中,∠C=90°,AC=6,BC=8,点P是△ABC的准内心(不包括顶点),且点P在△ABC的某条边上,则CP的长为。三、解答题(8小题,共78分)
-
19. 解不等式组,并将解集在数轴上表示出来,并写出最小整数解
 20. 已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向右平移5个单位长度,再F向下平移3个单位长度得到△A1B1C1(图中每个小方格边长均为1个单位长度)
20. 已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向右平移5个单位长度,再F向下平移3个单位长度得到△A1B1C1(图中每个小方格边长均为1个单位长度) (1)、在图中画出平移后的△A1B1C1;(2)、直接写出△A1B1C1各顶点的坐标A1 , B1 , C1 ,(3)、在x轴上找到一点M,当AM+A1M取最小值时,M点的坐标是 。21. 如图,已知点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AC∥DF。
(1)、在图中画出平移后的△A1B1C1;(2)、直接写出△A1B1C1各顶点的坐标A1 , B1 , C1 ,(3)、在x轴上找到一点M,当AM+A1M取最小值时,M点的坐标是 。21. 如图,已知点B,E,C,F在同一直线上,AB=DE,AC=DF,BE=CF.求证:AC∥DF。 22. 为了提倡低碳环保,北仑区某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元。(1)、求甲、乙两种型号设备的价格;(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司共有几种购买方案;(3)、在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买案。
22. 为了提倡低碳环保,北仑区某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购,经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元。(1)、求甲、乙两种型号设备的价格;(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司共有几种购买方案;(3)、在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月,若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买案。
23. 如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量y(千瓦时)关于已行驶路程x(千米)的函数图象。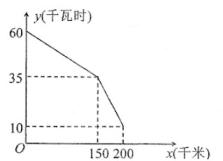 (1)、①根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程。
(1)、①根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程。②当0≤x≤150时,求1千瓦时的电量汽车能行驶的路程
(2)、当150≤x≤200时,求y关于x的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量。24. 已知,点P是等边△ABC中一点,以线段AP为边向右边作等边△APQ,连接PQ、QC。 (1)、求证:PB=QC;(2)、若PA=3,PB=4,∠APB=150°,求PC的长度。25. 定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足x= ,y= 那么称点T是点A,B的融合点。
(1)、求证:PB=QC;(2)、若PA=3,PB=4,∠APB=150°,求PC的长度。25. 定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足x= ,y= 那么称点T是点A,B的融合点。例如:A(-1,8),B(4,-2),当点T(x,y)满足x= =1,y= =2时,则点T(1,2)是点A,B的融合点。
 (1)、已知点A(-1,5),B(7,7),C(2,4),请说明其中一个点是另外两个点的融合点。(2)、如图,点D(3,0),点E(t,2+3)是直线l上任意一点,点T(x,y)是点D,E的融合点。
(1)、已知点A(-1,5),B(7,7),C(2,4),请说明其中一个点是另外两个点的融合点。(2)、如图,点D(3,0),点E(t,2+3)是直线l上任意一点,点T(x,y)是点D,E的融合点。①试确定y与x的关系式。
②若直线ET交x轴于点H,当△DTH为直角三角形时,求点E的坐标。
26. 如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒。
 (1)、出发2秒后,求△ABP的周长(2)、问t为何值时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、g中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成1:2的两部分?
(1)、出发2秒后,求△ABP的周长(2)、问t为何值时,△BCP为等腰三角形?(3)、另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、g中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成1:2的两部分?