浙江省温州市2019-2020学年九年级上学期数学期末考试试卷
试卷更新日期：2020-02-04 类型：期末考试
一、选择题(本题有10小题，每小题3分，共30分．)
-
1. 已知⊙O的半径为5cm，点P在⊙O上，则OP的长为（ ）A、4cm B、5cm C、8cm D、10cm2. 若 ，则 的值为（ ）A、 B、 C、 D、-3. 将抛物线y=x2-2向上平移1个单位后所得新抛物线的表达式为（ ）A、y=x2-1 B、y=x2-3 C、y=(x+1)2-2 D、y=(x-1)2-24. 如图，在5×6的方格纸中，画有格点△EFG，下列选项中的格点，与E，G两点构成的三角形中和△EFG相似的是（ ）
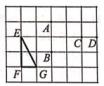A、点A B、点B C、点C D、点D5. 某单位进行内部抽奖，共准备了100张抽奖券，设一等奖10个，二等奖20个，三等奖30个。若每张抽奖券获奖的可能性相同，则1张抽奖券中奖的概率是（ ）A、0.1 B、0.2 C、0.3 D、0.66. 如图，∠ACB是⊙O的圆周角，若⊙O的半径为10，∠ACB=45°，则扇形AOB的面积为（ ）
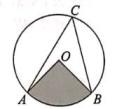A、5π B、12.5π C、20π D、25π7. 已知点A(-3，a)，B(-2，b)，C(1，c)均在抛物线y=3(x+2)2+k上，则a，b，c的大小关系是（ ）A、c<a<b B、a<c<b C、b<a<c D、b<c<a8. 如图，AD是⊙O的直径，以A为圆心，弦AB为半径画弧交⊙O于点C，连结BC交AD于点E，若DE=3，BC=8，则⊙O的半径长为（ ）
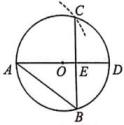A、 B、5 C、 D、9. 有一等腰三角形纸片ABC，AB=AC，裁剪方式及相关数据如图所示，则得到的甲、乙、丙、丁四张纸片中，面积最大的是（ ）
A、甲 B、乙 C、丙 D、丁10. 如图，抛物线y=-(x+m)2+5交x轴于点A，B，将该抛物线向右平移3个单位后，与原抛物线交于点C，则点C的纵坐标为（ ）
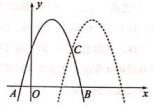A、 B、 C、3 D、二、填空题(本题有8个小题，每小题3分，共24分)
-
11. 抛物线y=x2-9与y轴的交点坐标为。12. 如图，是用卡钳测量容器内径的示意图．量得卡钳上A，D两端点的距离为4cm， ，则容器的内径BC的长为cm。
13. 如图，AB是半圆O的直径，∠BAC=20°，D是 上任意一点，则∠ADC=度。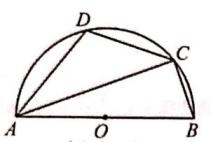
14. 如图，△ABC绕点A逆时针旋转得到△AB’C’点C在AB上，点C的对应点C在BC的延长线上，若∠BAC’=80°，则∠B=度。
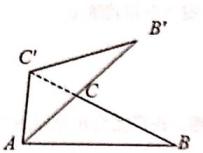15. 如图，正五边形 ABCDE内接于⊙O，若O的半径为10，则 的长为。
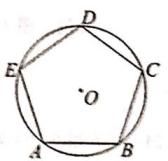16. 如图，在△ABC中，∠ABC=90°，AB=6，BC=4，P是△ABC的重心，连结BP，CP，则△BPC的面积为。
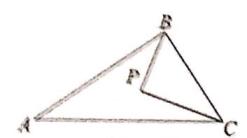17. 已知二次函数y=x2-4x+3，当a≤x≤a+5时，函数y的最小值为-1，则a的取值范围是。18. 如图，AB是半圆O的直径，D是半圆O上一点，C是 的中点，连结AC变BD于点E，连结AD，若BE=4DE，CE=6，则AB的长为。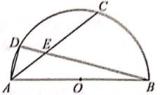
三、解答题（本题有6小题，共46分，)
-
19. 甲乙两人参加一个幸运挑战活动，活动规则是：一个布袋里装有3个只有颜色不同的球，其中2个红球，1个白球，甲从布袋中摸出一个球，记下颜色后放回，搅匀，乙再摸出一个球，若颜色相同，则挑战成功。(1)、用列表法或树状图法，表示所有可能出现的结果。(2)、求两人挑战成功的概率。20. 我们把端点都在格点上的线段叫做格点线段．如图，在7×7的方格纸中，有格点线段AB，按要求画图。
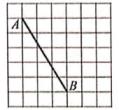(1)、在图1中画一条格点线段CD将AB平分(2)、在图2中画一条格点线段EF，将AB分为1：321. 如图，在平面直角坐标系中，抛物线y= x2+2x+a交x轴于点A，B，交y轴于点C，点A的横坐标为-2。
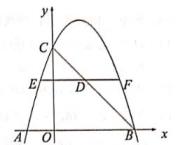(1)、求抛物线的对称轴和表达式。(2)、连结BC线段BC上有一点D，过点D作x轴的平行线交抛物线于点E，F，若EF=6，求点D的坐标。22. 如图，四边形ABCD内接于⊙O，点E在CB的延长线上，BA平分∠EBD，AE=AB，
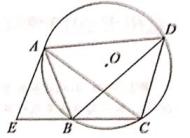(1)、求证：AC=AD。(2)、当 ，AD=6时，求CD的长。23. 总公司将一批衬衫由甲、乙两家分店共同销售，因地段不同，甲店一天可售出20件，每件盈利40元；乙店一天可售出32件，每件盈利30元，经调查发现，每件衬衫每降价1元，甲、乙两家店一天都可多售出2件，设甲店每件衬衫降价a元时，一天可盈利y1元，乙店每件衬衫降价b元时，一天可盈利y2元。(1)、当a=5时，求y1的值。(2)、求y2关于b的函数表达式。(3)、若总公司规定两家分店下降的价格必须相同，请求出每件衬衫下降多少元时，两家分店一天的盈利和最大，最大是多少元?24. 如图，在矩形ABCD中，AB=6，BC=8，点E，F分别在边BC，AB上，AF=BE=2，连结DE，DF，动点M在EF上从点E向终点F匀速运动，同时，动点N在射线CD上从点C沿CD方向匀速运动，当点M运动到EF的中点时，点N恰好与点D重合，点M到达终点时，M，N同时停止运动。
(1)、求EF的长。(2)、设CN=x，EM=y，求y关于x的函数表达式，并写出自变量x的取值范围。(3)、连结MN，当MN与△DEF的一边平行时，求CN的长。