辽宁省鞍山市台安县2020届九年级上学期数学第二次月考试卷
试卷更新日期:2020-02-04 类型:月考试卷
一、单选题
-
1. 在以下”绿色食品、响应环保、可回收物、节水“四个标志图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 关于x的一元二次方程kx2-3x+1=0有两个不相等的实数根,则k的取值范围( )A、 B、 且k≠0 C、 D、 且k≠03. 将抛物线y=(x-2)2+1向左平移2个单位,得到的新抛物线顶点坐标是( )A、 B、 C、 D、4. 若反比例函数 的图象经过点(﹣2,m),则m的值是( )A、 B、 C、 D、5. 如图1,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
2. 关于x的一元二次方程kx2-3x+1=0有两个不相等的实数根,则k的取值范围( )A、 B、 且k≠0 C、 D、 且k≠03. 将抛物线y=(x-2)2+1向左平移2个单位,得到的新抛物线顶点坐标是( )A、 B、 C、 D、4. 若反比例函数 的图象经过点(﹣2,m),则m的值是( )A、 B、 C、 D、5. 如图1,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
A、30° B、40° C、50° D、60°6. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( ) A、35° B、40° C、50° D、65°7. 一个圆锥的底面半径是5cm,其侧面展开图是圆心角是150°的扇形,则圆锥的母线长为( )A、9cm B、12cm C、15cm D、18cm8. 如图, 为等边三角形,点 从A出发,沿 作匀速运动,则线段 的长度y与运动时间x之间的函数关系大致是( )
A、35° B、40° C、50° D、65°7. 一个圆锥的底面半径是5cm,其侧面展开图是圆心角是150°的扇形,则圆锥的母线长为( )A、9cm B、12cm C、15cm D、18cm8. 如图, 为等边三角形,点 从A出发,沿 作匀速运动,则线段 的长度y与运动时间x之间的函数关系大致是( ) A、
A、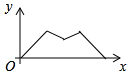 B、
B、 C、
C、 D、
D、
二、填空题
-
9. 关于x的反比例函数 的图像位于第二、四象限,则m的取值范围是 .10. 某市为了扎实落实脱贫攻坚中“两不愁、三保障”的住房保障工作,去年已投入5亿元资金,并计划投入资金逐年增长,明年将投入7.2亿元资金用于保障性住房建设,则这两年投入资金的年平均增长率为.11. 已知正六边形的外接圆的半径是 ,则正六边形的周长是 .12. 如图,边长为2的正三角形ABO的边OB在x轴上,将 绕原点O逆时针旋转 得到 ,则点 的坐标为 .
 13. 如图, 直径 ,点 , 是圆上两点, ,则弧 长为 .
13. 如图, 直径 ,点 , 是圆上两点, ,则弧 长为 .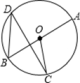 14. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
14. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .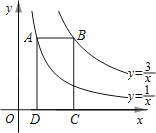 15. 如图,抛物线 (a,b,c是常数, )与x轴交于A,B两点,顶点 .给出下列结论:① ;②若 , , 在抛物线上,则 ;③关于x的方程 有实数解,则 ;④当 时, 为等腰直角三角形.其中正确结论是(填写序号).
15. 如图,抛物线 (a,b,c是常数, )与x轴交于A,B两点,顶点 .给出下列结论:① ;②若 , , 在抛物线上,则 ;③关于x的方程 有实数解,则 ;④当 时, 为等腰直角三角形.其中正确结论是(填写序号).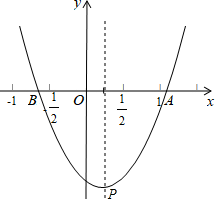 16. 如图已知等边 ,顶点 在双曲线 上,点 的坐标为 .过 作 交双曲线于点 ,过 作 交x轴于点 得到第二个等边 ;过 作 交双曲线于点 ,过 作 交x轴于点 ,得到第三个等边 ;以此类推,…,则点 的坐标为 .
16. 如图已知等边 ,顶点 在双曲线 上,点 的坐标为 .过 作 交双曲线于点 ,过 作 交x轴于点 得到第二个等边 ;过 作 交双曲线于点 ,过 作 交x轴于点 ,得到第三个等边 ;以此类推,…,则点 的坐标为 .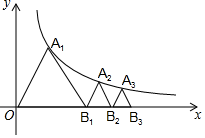
三、解答题
-
17. 用公式法解方程: .18. 在平面直角坐标系中, 的位置如图所示.(每个小方格都是边长为1个单位长度的正方形)
 (1)、①画出 关于y轴对称的 ;
(1)、①画出 关于y轴对称的 ;②将 绕点B逆时针旋转 ,画出旋转后得到的 ;
(2)、请直接写出线段BA变换到 过程中扫过区域的面积(结果保留 ).19. 已知关于x的一元二次方程x2﹣4 x+12+m=0.(1)、若方程的一个根是 ,求m的值及方程的另一根;(2)、若方程的两根恰为等腰三角形的两腰,而这个三角形的底边为m,求m的值及这个等腰三角形的周长.20. 如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点 表示火炬位置,火炬从离北京路10米处的M点开始传道,到离北京路1000米的N点时传递活动结束.迎圣火临时指挥部设在坐标原点O(北京路与奥运路的十字路口),OATB为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000(路线宽度均不计). (1)、求图中反比例函数的关系式(不需写出自变量的取值范围);(2)、当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示).21. 山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?22. 如图,已知一次函数 与反比例函数 的图象相交于点 ,与x轴相交于点B.
(1)、求图中反比例函数的关系式(不需写出自变量的取值范围);(2)、当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示).21. 山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)、每千克核桃应降价多少元?(2)、在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?22. 如图,已知一次函数 与反比例函数 的图象相交于点 ,与x轴相交于点B. (1)、求k的值;(2)、以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;(3)、观察反比例函数 的图象,请直接写出:当 时,自变量x的取值范围.23. 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)、求k的值;(2)、以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;(3)、观察反比例函数 的图象,请直接写出:当 时,自变量x的取值范围.23. 如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F. (1)、求证:CF是⊙O的切线;(2)、若∠F=30°,EB=8,求图中阴影部分的面积.(结果保留根号和π)24. 如图,斜坡AB长10米,按图中的直角坐标系可用 表示,点A,B分别在x轴和y轴上,且 .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用 表示.
(1)、求证:CF是⊙O的切线;(2)、若∠F=30°,EB=8,求图中阴影部分的面积.(结果保留根号和π)24. 如图,斜坡AB长10米,按图中的直角坐标系可用 表示,点A,B分别在x轴和y轴上,且 .在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用 表示.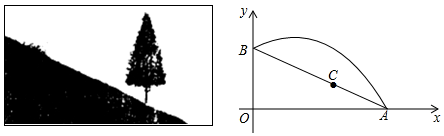 (1)、求抛物线的函数关系式(不必写自变量取值范围);(2)、求水柱离坡面AB的最大高度;(3)、在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?25. 如图①,E在AB上, 、 都为等腰直角三角形, ,连接DB,以DE、DB为边作平行四边形DBFE,连接FC、DC.
(1)、求抛物线的函数关系式(不必写自变量取值范围);(2)、求水柱离坡面AB的最大高度;(3)、在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?25. 如图①,E在AB上, 、 都为等腰直角三角形, ,连接DB,以DE、DB为边作平行四边形DBFE,连接FC、DC.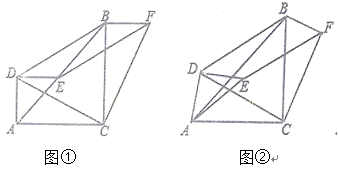 (1)、求证: ; ;(2)、将图①中 绕A点顺时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.(3)、将图①中的 绕A点顺时针旋转 , ,其它条件不变,当四边形DBFE为矩形时,直接写出 的值.26. 如图,抛物线y=x2﹣mx﹣(m+1)与x轴负半轴交于点A(x1 , 0),与x轴正半轴交于点B(x2 , 0)(OA<OB),与y轴交于点C,且满足x12+x22﹣x1x2=13.
(1)、求证: ; ;(2)、将图①中 绕A点顺时针旋转,其它条件不变,如图②,(1)中的结论是否成立?说明理由.(3)、将图①中的 绕A点顺时针旋转 , ,其它条件不变,当四边形DBFE为矩形时,直接写出 的值.26. 如图,抛物线y=x2﹣mx﹣(m+1)与x轴负半轴交于点A(x1 , 0),与x轴正半轴交于点B(x2 , 0)(OA<OB),与y轴交于点C,且满足x12+x22﹣x1x2=13. (1)、求抛物线的解析式;(2)、以点B为直角顶点,BC为直角边作Rt△BCD,CD交抛物线于第四象限的点E,若EC=ED,求点E的坐标;(3)、在抛物线上是否存在点Q,使得S△ACQ=2S△AOC?若存在,求出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的解析式;(2)、以点B为直角顶点,BC为直角边作Rt△BCD,CD交抛物线于第四象限的点E,若EC=ED,求点E的坐标;(3)、在抛物线上是否存在点Q,使得S△ACQ=2S△AOC?若存在,求出点Q的坐标;若不存在,说明理由.