辽宁省丹东市东港市六校2020届九年级上学期数学12月月考试卷
试卷更新日期:2020-02-04 类型:月考试卷
一、单选题
-
1. 如图,CD为Rt△ABC斜边上的高,如果AD=6,BD=2,那么CD等于( )
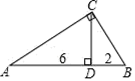 A、2 B、4 C、 D、2. 如图,下列条件不能判定△ADB∽△ABC的是( )
A、2 B、4 C、 D、2. 如图,下列条件不能判定△ADB∽△ABC的是( )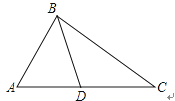 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、3. 若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y= (k<0)上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y24. 如图,点O是矩形ABCD的对角线AC的中点, 交AD于点M,若 , ,则OB的长为
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、3. 若点(﹣2,y1),(﹣1,y2),(3,y3)在双曲线y= (k<0)上,则y1 , y2 , y3的大小关系是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y24. 如图,点O是矩形ABCD的对角线AC的中点, 交AD于点M,若 , ,则OB的长为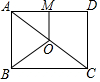 A、4 B、5 C、6 D、5. 关于 的一元二次方程 有两个实数根,则 的取值范围是( )A、k≥0 B、k≤0 C、k<0且 D、k≤0且6. 如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )
A、4 B、5 C、6 D、5. 关于 的一元二次方程 有两个实数根,则 的取值范围是( )A、k≥0 B、k≤0 C、k<0且 D、k≤0且6. 如图,在平行四边形ABCD中,E是DC上的点,DE:EC=3:2,连接AE交BD于点F,则△DEF与△BAF的面积之比为( )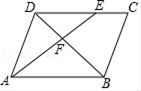 A、2:5 B、3:5 C、9:25 D、4:257. 如图,点 在 轴正半轴上运动,点 在 轴上运动,过点 且平行于 轴的直线分别交函数 和 于 、 两点,则三角形 的面积等于( )
A、2:5 B、3:5 C、9:25 D、4:257. 如图,点 在 轴正半轴上运动,点 在 轴上运动,过点 且平行于 轴的直线分别交函数 和 于 、 两点,则三角形 的面积等于( ) A、1 B、2 C、3 D、68. 如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )
A、1 B、2 C、3 D、68. 如图,在菱形ABCD中,AC=6 ,BD=6,E是BC边的中点,P,M分别是AC,AB上的动点,连接PE,PM,则PE+PM的最小值是( )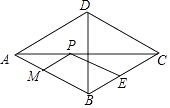 A、6 B、3 C、2 D、4.5
A、6 B、3 C、2 D、4.5二、填空题
-
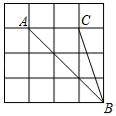
9. 一元二次方程x2﹣x=0的根是 .10. 关于 的一元二次方程 的一个根为0,则 的值.11. 如图,正方形网格中每个小正方形的边长都是1,若点A、B、C都在格点上,则tan∠BAC的值是.
 12. 如图,一艘轮船自西向东航行,航行到A处测得小岛C位于北偏东60°方向上,继续向东航行10海里到达点B处,测得小岛C在轮船的北偏东15°方向上,此时轮船与小岛C的距离为海里.(结果保留根号)
12. 如图,一艘轮船自西向东航行,航行到A处测得小岛C位于北偏东60°方向上,继续向东航行10海里到达点B处,测得小岛C在轮船的北偏东15°方向上,此时轮船与小岛C的距离为海里.(结果保留根号)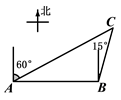 13. 如图, 与 是以点 为位似中心的位似图形,相似比为 , , ,若点 的坐标是 ,则点 的坐标是.
13. 如图, 与 是以点 为位似中心的位似图形,相似比为 , , ,若点 的坐标是 ,则点 的坐标是.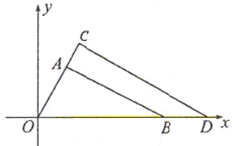 14. 如图,菱形ABCD的面积为6,边AD在x轴上,边BC的中点E在y轴上,反比例函数 的图象经过顶点B,则k的值为 .
14. 如图,菱形ABCD的面积为6,边AD在x轴上,边BC的中点E在y轴上,反比例函数 的图象经过顶点B,则k的值为 . 15. 已知正方形 的边长为6,点 , 分别在 , 上, , 与 相交于点 ,点 为 的中点,连接 ,则 的长为.
15. 已知正方形 的边长为6,点 , 分别在 , 上, , 与 相交于点 ,点 为 的中点,连接 ,则 的长为.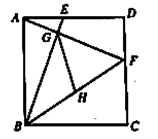 16. 如图,点P是正方形ABCD的对角线BD延长线上的一点,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中:①PA=PE;②CE= PD;③BF﹣PD= BD;④S△PEF=S△ADP , 正确的是(填写所有正确结论的序号)
16. 如图,点P是正方形ABCD的对角线BD延长线上的一点,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F,则下列结论中:①PA=PE;②CE= PD;③BF﹣PD= BD;④S△PEF=S△ADP , 正确的是(填写所有正确结论的序号)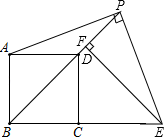
三、解答题
-
17.(1)、解方程:(2)、计算:18. 已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中, 每个小正方形的边长是1个单位长度)
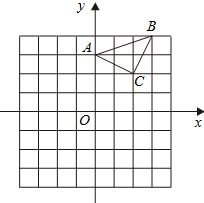
① 画出△ABC向下平移4个单位得到的△A1B1C1 , 并直接写出C1点的坐标;
②以点B为位似中心,在网格中画出△A2BC2 , 使△A2BC2与△ABC位似,且位似比为2︰1,并直接写出C2点的坐标及△A2BC2的面积.
19. 如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)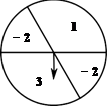 (1)、转动转盘一次,求转出的数字是-2的概率;(2)、转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.20. 某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.(1)、求每次下降的百分率;(2)、若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?21. 小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为 ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据: )
(1)、转动转盘一次,求转出的数字是-2的概率;(2)、转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.20. 某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.(1)、求每次下降的百分率;(2)、若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?21. 小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为 ,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为 .已知山坡坡度 ,即 ,请你帮助小明计算古塔的高度ME.(结果精确到0.1m,参考数据: ) 22. 如图,在平面直角坐标系中,点 在反比例函数 的图象上, , 轴于点C.
22. 如图,在平面直角坐标系中,点 在反比例函数 的图象上, , 轴于点C.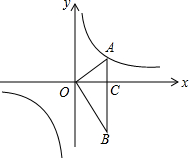 (1)、求反比例函数 的表达式;(2)、求 的面积;(3)、若将 绕点B按逆时针方向旋转 得到 点O、A的对应点分别为 、 ,点 是否在反比例函数 的图象上?若在请直接写出该点坐标,若不在请说明理由.23. 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
(1)、求反比例函数 的表达式;(2)、求 的面积;(3)、若将 绕点B按逆时针方向旋转 得到 点O、A的对应点分别为 、 ,点 是否在反比例函数 的图象上?若在请直接写出该点坐标,若不在请说明理由.23. 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG. (1)、求证:四边形EFDG是菱形;(2)、求证: ;(3)、若AG=6,EG=2 ,求BE的长.24. 在矩形ABCD中, , ,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为 ,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
(1)、求证:四边形EFDG是菱形;(2)、求证: ;(3)、若AG=6,EG=2 ,求BE的长.24. 在矩形ABCD中, , ,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为 ,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.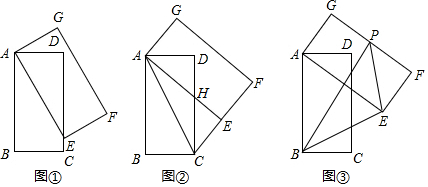 (1)、如图 ,当点E落在DC边上时,直写出线段EC的长度为;(2)、如图 ,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
(1)、如图 ,当点E落在DC边上时,直写出线段EC的长度为;(2)、如图 ,当点E落在线段CF上时,AE与DC相交于点H,连接AC,求证: ≌ ;
直接写出线段DH的长度为.
(3)、如图 设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中, 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.