湖北省孝感市八校联谊2020届九年级上学期数学12月月考试卷

试卷更新日期：2020-02-04 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 用配方法解方程 $x^{2} - 2 x - 1 = 0$ 时，配方后所得的方程为（）

A、 $（ x + 1 ）^{2} = 0$ B、 $（ x - 1 ）^{2} = 0$ C、 $（ x + 1 ）^{2} = 2$ D、 $（ x - 1 ）^{2} = 2$

查看试题解析
3. 如图，在平面直角坐标系中，点B，C，E，在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（）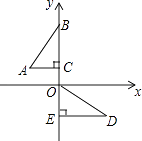

A、△ABC绕点C顺时针旋转90°，再向下平移3 B、△ABC绕点C顺时针旋转90°，再向下平移1 C、△ABC绕点C逆时针旋转90°，再向下平移1 D、△ABC绕点C逆时针旋转90°，再向下平移3

查看试题解析
4. 若关于x的一元二次方程(k－1)x²＋4x＋1＝0有两个不相等的实数根，则k的取值范围是（）

A、k<5 B、k<5，且k≠1 C、k≤5，且k≠1 D、k>5

查看试题解析
5. 若二次函数y=x²+2x+c配方后为y=（x+h）²+7，则c、h的值分别为（）

A、8、-1 B、8、1 C、6、-1 D、6、1

查看试题解析
6. 如图，在⊙O中，AB为直径，圆周角∠ACD=20°，则∠BAD等于（）

A、20° B、40° C、70° D、80°

查看试题解析
7. 若抛物线y=x²﹣2x+3不动，将平面直角坐标系xOy先沿水平方向向右平移一个单位，再沿铅直方向向上平移三个单位，则原抛物线图象的解析式应变为（　　）

A、y=（x﹣2）²+3 B、y=（x﹣2）²+5 C、y=x²﹣1 D、y=x²+4

查看试题解析
8. 如图， $O A$ 为 $⊙ O$ 半径，点 $P$ 为 $O A$ 中点， $Q$ 为 $⊙ O$ 上一点，且 $∠ A P Q = 135 °$ ，若 $O A = 2$ ，则 $P Q$ 的长为（）

A、 $\frac{5}{2}$ B、 $\sqrt{14}$ C、 $3 \sqrt{2}$ D、 $\frac{\sqrt{14} + \sqrt{2}}{2}$

查看试题解析
9. 如图，等腰 $Rt △ A B C$ ，点 $O$ 为斜边 $A C$ 上，作 $⊙ O$ 与 $A B$ 相切于点 $D$ ，交 $B C$ 于点 $E$ 、点 $F$ ．已知 $A B = B C = 9$ ， $C F = 1$ ，则 $B E$ 的长度为（）

A、 $1$ B、 $2$ C、 $3$ D、 $5$

查看试题解析
10. 如图，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的顶点为B(1，3)，与 $x$ 轴的交点A在点 (2，0)和(3，0)之间．以下结论：
① $a b c > 0$ ；② $a - b + c < 0$ ；③ $2 a + b = 0$ ；④ $a + b$ ≥ $a m^{2} + b m$ ；⑤若 $a x_{1}^{2} + b x_{1} = a x_{2}^{2} + b x_{2}$ ，且 $x_{1} \neq x_{2}$ ，

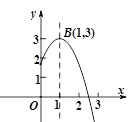
则 $x_{1} + x_{2} = 2$ .其中正确的结论有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 已知点 $(a, - 1)$ 与点 $(2, b)$ 关于原点对称，则 $a + b =$

查看试题解析
12. 二次函数 $y = x^{2} - 2 x - 3$ 的顶点坐标为．

查看试题解析
13. 如图，有一块长30 m、宽20 m的矩形田地，准备修筑同样宽的三条直路，把田地分成六块，种植不同品种的蔬菜，并且种植蔬菜面积为矩形田地面积的，则道路的宽为

查看试题解析
14. 已知圆锥的底面半径为40cm，母线长为90cm，则它的侧面展开图的圆心角为．

查看试题解析
15. 如图，正方形 $A B C D$ 中， $A B = 5$ ，点 $E$ 、 $F$ 分别在 $B C$ 、 $C D$ 上， $B E = 3$ ， $∠ B A E + ∠ D A F = ∠ E A F$ ，则 $△ A E F$ 的面积是．

查看试题解析
16. 点 P 是抛物线 $y = - x^{2} + 5 x + 3$ 的图象上一点，过 P 向 x 轴作垂线，垂足为点 Q ，当点 P 在第一象限抛物线上运动的过程中， $O Q + P Q$ 的值最大时，点 P 的坐标．

查看试题解析

三、解答题

17. 解方程：

(1)、x²+2x﹣1=0

(2)、x（x+4）=3x+12．

查看试题解析
18. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (1 ， 1)$ 、 $B (4 ， 2)$ 、 $C (3 ， 4)$ ．

① 请画出将 $△ A B C$ 向左平移 $4$ 个单位长度后得到的图形 $△ A_{1} B_{1} C_{1}$ ，直接写出点 $A_{1}$ 的坐标；

② 请画出 $△ A_{1} B_{1} C_{1}$ 绕原点 $O$ 顺时针旋转 $90 °$ 的图形 $△ A_{2} B_{2} C_{2}$ ，直接写出点 $A_{2}$ 的坐标；

③在 $x$ 轴上找一点 $P$ ，使 $P A + P B$ 的值最小，请直接写出点 $P$ 的坐标．

查看试题解析
19. 如图，两个圆都是以 $O$ 为圆心．

(1)、求证： $A C = B D$ ；

(2)、若 $A B = 10$ ， $B D = 2$ ，小圆的半径为 $5$ ，求大圆的半径 $R$ 的值．

查看试题解析
20. 如图，把△ABC 绕点 A 顺时针旋转 n 度（0＜n＜180）后得到△ADE，并使点 D 落在 AC 的延长线上．

(1)、若∠B=17°，∠E=55°，求 n；

(2)、若 F 为 BC 的中点，G 为 DE 的中点，连 AG、AF、FG，求证：△AFG 为等腰三角形．

查看试题解析
21. 已知△ABC的两边AB、AC的长恰好是关于x的方程x²＋(2k＋3)x＋k²＋3k＋2＝0的两个实数根，第三边BC的长为5

(1)、求证：AB≠AC

(2)、如果△ABC是以BC为斜边的直角三角形，求k的值

(3)、填空：当k＝时，△ABC是等腰三角形，△ABC的周长为

查看试题解析
22. 某商场销售的某种商品每件的标价是 $80$ 元，若按标价的八折销售，仍可盈利 $60 %$ ，此时该种商品每星期可卖出 $220$ 件，市场调查发现：在八折销售的基础上，该种商品每降价 $1$ 元，每星期可多卖 $20$ 件．设每件商品降价 $x$ 元（ $x$ 为整数），每星期的利润为 $y$ 元

(1)、求该种商品每件的进价为多少元？

(2)、当售价为多少时，每星期的利润最大？最大利润是多少？

(3)、2019年2月该种商品每星期的售价均为每件 $m$ 元，若2019年2月的利润不低于 $24000$ 元，请求出 $m$ 的取值范围．

查看试题解析
23. 如图1， $A B$ 是 $⊙ O$ 的直径， $A C$ 是弦，点 $P$ 是 $\overset{⌢}{B C}$ 的中点， $P E ⊥ A C$ 交 $A C$ 的延长线于 $E$ ．

(1)、求证： $P E$ 是 $⊙ O$ 的切线；

(2)、如图2，作 $P H ⊥ A B$ 于 $H$ ，交 $B C$ 于 $N$ ，若 $N H = 3$ ， $B H = 4$ ，求 $P E$ 的长．

查看试题解析
24. 综合与探究
如图，抛物线 $y = a x^{2} + b x + 6$ 经过点A(-2，0)，B(4，0)两点，与 $y$ 轴交于点C，点D是抛物线上一个动点，设点D的横坐标为 $m (1 < m < 4)$ .连接AC，BC，DB，DC.

(1)、求抛物线的函数表达式；

(2)、△BCD的面积等于△AOC的面积的 $\frac{3}{4}$ 时，求 $m$ 的值；

(3)、在(2)的条件下，若点M是 $x$ 轴上的一个动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B，D，M，N为顶点的四边形是平行四边形，若存在，请直接写出点M的坐标；若不存在，请说明理由.

查看试题解析