江苏省连云港市灌云县2020届九年级上学期数学第二次月考试卷

试卷更新日期：2020-02-04 类型：月考试卷

进入出卷网下载

一、单选题

1. 二次函数y＝2x²﹣3的二次项系数、一次项系数和常数项分別是（）

A、2、0、﹣3 B、2、﹣3、0 C、2、3、0 D、2、0、3

查看试题解析
2. 数据4，3，5，3，6，3，4的众数和中位数是（）

A、3，4 B、3，5 C、4，3 D、4，5

查看试题解析
3. 四张质地、大小相同的卡片上，分别画上如图所示的四种汽车标志，在看不到图形的情况下从中任意抽出一张，则抽出的卡片既是中心对称图形，又是轴对称图形的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、1

查看试题解析

4. 如表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数 $\bar{x}$ （厘米）	$375$	$350$	$375$	$350$
方差 $s^{2}$	$12.5$	$13.5$	$2.4$	$5.4$

要从中选择一名成绩好又发挥稳定的运动员参加决赛，最合适的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

5. 关于概率，下列说法正确的是（）

A、某地“明天降雨的概率是90%”表明明天该地有90%的时间会下雨； B、13个同学参加一个聚会，他们中至少有两个同学的生日在同一个月； C、“打开电视，正在播放新闻节目”是不可能事件； D、经过有交通信号灯的路口，一定遇到红灯.

查看试题解析
6. 关于抛物线 $y = 2 {(x + 3)}^{2}$ ，以下说法正确的是（）

A、开口向下 B、对称轴是x= —3 C、顶点坐标是（0，0） D、当x＞—3时，y随x增大而减小

查看试题解析
7. 如图是王阿姨晚饭后步行的路程s(单位：m)与时间t(单位：min)的函数图象，其中曲线段AB是以B为顶点的抛物线一部分.下列说法不正确的是（）

A、25min~50min，王阿姨步行的路程为800m B、线段CD的函数解析式为 $s = 32 t + 400 （ 25 \leq t \leq 50 ）$ C、5min~20min，王阿姨步行速度由慢到快 D、曲线段AB的函数解析式为 $s = - 3 （ t - 20 ）^{2} + 1200 （ 5 \leq t \leq 20 ）$

查看试题解析

8. 抛物线y＝ax²+bx+c（a≠0，a、b、c为常数）上部分点的横坐标x，纵坐标y的对应值如下表：

x	……	﹣3	﹣2	﹣1	0	1	2	……
y	……	$\frac{5}{2}$	4	$\frac{9}{2}$	4	m	0	……

则下列结论中：①抛物线的对称轴为直线x＝﹣1；②m＝ $\frac{5}{2}$ ；③当﹣4＜x＜2时，y＜0；④方程ax²+bx+c﹣4＝0的两根分别是x₁＝﹣2，x₂＝0，其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

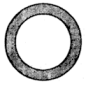
9. 请你写出一个开口向下，且与 $y$ 轴的交点坐标为 $(0 ， 3)$ 的二次函数的解析式：.

查看试题解析
10. 数学老师计算同学们一学期的平均成绩时，将平时、期中和期末的成绩按3:3:4计算，若小红平时、期中和期末的成绩分别是90分、100分、90分，则小红一学期的数学平均成绩是分．

查看试题解析
11. 小明用S²= $\frac{1}{10}$ [（x₁﹣3）²+（x₂﹣3）²+…+（x₁₀﹣3）³]计算一组数据的方差，那么x₁+x₂+x₃+…+x₁₀= ．

查看试题解析
12. 如图，墙上有一个同心圆纸板，大圆的半径为40cm，小圆的半径为30cm，若向这个纸板投掷飞镖（每次飞镖均落在纸板上），则飞镖落在阴影区域的概率为.

查看试题解析
13. 将抛物线 $y = x^{2}$ 先向右平移1个单位长度，再向上平移2个单位长度，得到的抛物线的解析式是.

查看试题解析
14. 二次函数y₁＝ax²+bx+c与一次函数y₂＝mx+n的图象如图所示，则满足ax²+bx+c≥mx+n的x的取值范围是．

查看试题解析
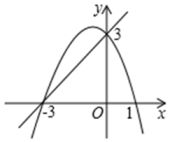15. 如图，经过抛物线y＝x²+x﹣2与坐标轴交点的圆与抛物线另交于点D，与y轴另交于点E，则∠BED＝．

查看试题解析
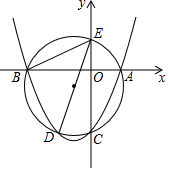16. 二次函数y＝2x²的图象如图所示，坐标原点O，点B₁ ， B₂ ， B₃在y轴的正半轴上，点A₁ ， A₂ ， A₃在二次函数y＝2x²位于第一象限的图象上，若△A₁OB₁ ， △A₂B₁B₂ ， △A₃B₂B₃都为等腰直角三角形，且点A₁ ， A₂ ， A₃均为直角顶点，则点A₃的坐标是．

查看试题解析

三、解答题

17. 已知y关于 x的函数y=（m²+2m）x²+mx+m+1.

(1)、当m为何值时，此函数是一次函数？

(2)、当m为何值时，此函数是二次函数？

查看试题解析
18. 已知，抛物线的顶点坐标为（2，1），与y轴交于点（0，3）．求

(1)、这条抛物线的表达式；

(2)、直接写出当1＜x＜5时，y的取值范围为．

查看试题解析
19. 某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛，射击队对两人的射击技能进行了测评．在相同的条件下，两人各打靶5次，成绩统计如下：

(1)、填写下表：

平均数（环）

中位数（环）

方差（环²）

君君

8

0.4

标标

8

(2)、根据以上信息，若选派一名队员参赛，你认为应选哪名队员，并说明理由．

(3)、如果标标再射击1次，命中8环，那么他射击成绩的方差会．（填“变大”“变小”或“不变”）

查看试题解析
20. 如图，已知二次函数 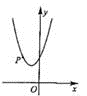$y = x^{2} + a x + 3$ 的图象经过点 $P (- 2 ， 3)$ .

(1)、求 $a$ 的值和图象的顶点坐标。

(2)、点 $Q (m ， n)$ 在该二次函数图象上.
①当 $m = 2$ 时，求 $n$ 的值；

②若 $Q$ 到 $y$ 轴的距离小于2，请根据图象直接写出 $n$ 的取值范围.

查看试题解析
21. 某初中对 600 名毕业生中考体育测试坐位体前屈成绩进行整理，绘制成如下不完整的统计图：

根据统计图，回答下列问题。

(1)、请将条形统计图补充完整；

(2)、扇形统计图中，b= ，得 8 分所对应扇形的圆心角度数为；

(3)、在本次调查的学生中，随机抽取 1 名男生，他的成绩不低于 9 分的概率为多少？

查看试题解析
22. 已知抛物线y=ax2+bx+c 如图所示，直线x=-1是其对称轴，

(1)、确定a，b，c，Δ=b2-4ac的符号

(2)、求证：a-b+c>0

(3)、当x取何值时，y>0；当x取何值时y<0.

查看试题解析
23. 中国古代有着辉煌的数学成就，《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.

(1)、小聪想从这4部数学名著中随机选择1部阅读，求他选中《九章算术》的概率；

(2)、小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容，用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.

查看试题解析
24. 有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为4m，跨度为10m，如图所示，把它的图形放在直角坐标系中．

(1)、求这条抛物线所对应的函数关系式；

(2)、一辆宽为2米，高为3米的货船能否从桥下通过？

查看试题解析
25. 某超市以20元/千克的进货价购进了一批绿色食品，如果以30元/千克销售这些绿色食品，那么每天可售出400千克.由销售经验可知，每天的销售量y（千克）与销售单价x（元）（x≥30）存在如图所示的一次函数关系.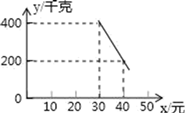

(1)、试求出y与x的函数关系式；

(2)、设该超市销售该绿色食品每天获得利润w元，当销售单价为何值时，每天可获得最大利润？最大利润是多少？

查看试题解析
26. 如图，已知抛物线经过两点A（﹣3，0），B（0，3），且其对称轴为直线x＝﹣1．

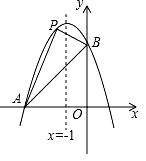(1)、求此抛物线的解析式．

(2)、若点Q是对称轴上一动点，当OQ+BQ最小时，求点Q的坐标．

(3)、若点P是抛物线上点A与点B之间的动点（不包括点A，点B），求△PAB面积的最大值，并求出此时点P的坐标．

查看试题解析

	平均数（环）	中位数（环）	方差（环²）
君君		8	0.4
标标	8