江苏省盐城市东台市2020届九年级上学期数学12月月考试卷
试卷更新日期:2020-02-04 类型:月考试卷
一、单选题
-
1. 抛物线 的顶点坐标是( )A、(2,3) B、(-2,3) C、(2,-3) D、(-2,-3)2. 若一元二次方程x2﹣2x+m=0有两个不相同的实数根,则实数m的取值范围是( )A、m≥1 B、m≤1 C、m>1 D、m<13. 盒子中装有1个红球和2个绿球,每个球除颜色外完全相同,从盒子中任意摸出一个球,是红球的概率是( )A、 B、 C、 D、4. 若方程 的两实根为 ,则 的值为( )A、-3 B、3 C、-4 D、45. 将抛物线 向上平移2个单位,所得抛物线的表达式为( )A、 B、 C、 D、6. 若二次函数y=x2-6x+c的图象过A(-1,y1),B(2,y2),C(3+ ,y3)三点,则y1,y2,y3大小关系正确的是( )
A、y1>y2>y3 B、y1>y3>y2 C、y 2>y1>y3 D、y3>y1>y27. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( ) A、15
A、15 B、28
B、28  C、29
C、29  D、34
D、34  8.
8.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是( )
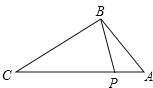 A、∠ABP=∠C B、∠APB=∠ABC C、 D、
A、∠ABP=∠C B、∠APB=∠ABC C、 D、二、填空题
-
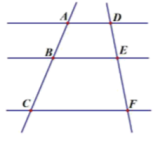
9. 圆锥的底面半径是 ,母线长为 ,则这个圆锥的侧面积是 (结果保留 )10. 已知 ,则 的值为.11. 如图,已知: , , , ,则
 12. 若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .13. 地球上陆地与海洋的面积比是 ,宇宙一块陨石落入地球,落在陆地的概率是.14. 已知二次函数 中,函数y与x的部分对应值如下:
12. 若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .13. 地球上陆地与海洋的面积比是 ,宇宙一块陨石落入地球,落在陆地的概率是.14. 已知二次函数 中,函数y与x的部分对应值如下:...
-1
0
1
2
3
...
...
10
5
2
1
2
...
则当 时,x的取值范围是.
15. 直角三角形斜边长为6,那么这个三角形的重心到斜边中点的距离为.16. 抛物线 (a、b、c为常数,且 )经过点 和 ,且 ,当 时,y随着x的增大而减小.下列结论:① ;② ;③若点 、点 都在抛物线上,则 ;④ ;⑤若 ,则 .其中结论正确的是.(只填写序号)三、解答题
-
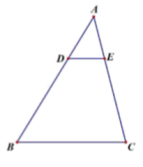
17. 解方程(1)、(2)、 ;18. 四张扑克牌的点数分别是4、5、6、10,将它们洗匀后背面朝上放在桌面上.(1)、从中随机抽取一张牌,求这张牌的点数是偶数的概率是.(2)、从中先随机抽取一张牌(不放回),接着再抽取一张牌,求这两张牌的点数都是偶数的概率.19. 关于 的方程 .(1)、求证:不论 为何值,方程总有两个不相等的实数根;(2)、若方程有一个根是1,求另一个根及 的值.20. 如图,在 中,已知 , , , ,求DE的长.
 21. 某工厂1月份的产值是25万元,计划3月份的产值达到36万元,那么这家工厂2月、3月这两个月产值的月平均的增长率是多少?22. 已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
21. 某工厂1月份的产值是25万元,计划3月份的产值达到36万元,那么这家工厂2月、3月这两个月产值的月平均的增长率是多少?22. 已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD. (1)、求证:AD是∠BAC的平分线;(2)、若AC= 3,BC=4,求⊙O的半径.23. 已知二次函数 .
(1)、求证:AD是∠BAC的平分线;(2)、若AC= 3,BC=4,求⊙O的半径.23. 已知二次函数 .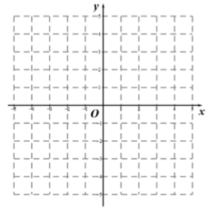 (1)、求抛物线顶点M的坐标;(2)、设抛物线与x轴交于A、B两点,与y轴交于C点,求A、B、C的坐标(点A在点B的左侧),并画出函数图象的大致示意图;(3)、根据图像,写出不等式 的解集.24. 如图,四边形ABCD、CDEF、EFGH都是正方形.
(1)、求抛物线顶点M的坐标;(2)、设抛物线与x轴交于A、B两点,与y轴交于C点,求A、B、C的坐标(点A在点B的左侧),并画出函数图象的大致示意图;(3)、根据图像,写出不等式 的解集.24. 如图,四边形ABCD、CDEF、EFGH都是正方形.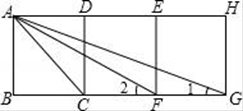 (1)、△ACF与△ACG相似吗?说说你的理由.(2)、求∠1+∠2的度数.25. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示.
(1)、△ACF与△ACG相似吗?说说你的理由.(2)、求∠1+∠2的度数.25. “扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量 (件)与销售单价 (元)之间存在一次函数关系,如图所示.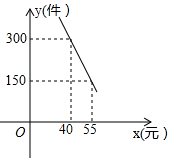 (1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.26. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)、求 与 之间的函数关系式;(2)、如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.26. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”. (1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= ;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)、如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.27. 如图1,对称轴为直线x=1的抛物线y= x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= ;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)、如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.27. 如图1,对称轴为直线x=1的抛物线y= x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.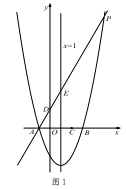
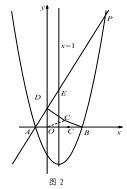 (1)、求点 B 的坐标和抛物线的表达式;(2)、当 AE:EP=1:4 时,求点 E 的坐标;(3)、如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ C′D 的最小值.
(1)、求点 B 的坐标和抛物线的表达式;(2)、当 AE:EP=1:4 时,求点 E 的坐标;(3)、如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ C′D 的最小值.