2016-2017学年湖北省宜昌市七校教学协作体高一下学期期末数学试卷

试卷更新日期：2017-08-07 类型：期末考试

进入出卷网下载

一、选择题

1. 已知a＞b＞0且c＜d，下列不等式中成立的一个是（）

A、a+c＞b+d B、a﹣c＞b﹣d C、ad＜bc D、 $\frac{a}{c}$ ＞ $\frac{b}{d}$

查看试题解析
2. 已知向量 $\vec{a}$ =（4，2），向量 $\vec{b}$ =（x，3），且 $\vec{a} ∥ \vec{b}$ ，那么x等于（）

A、8 B、7 C、6 D、5

查看试题解析
3. 在△ABC中，a=2 $\sqrt{3}$ ，b=2 $\sqrt{2}$ ，∠B=45°，则∠A=（）

A、30°或120° B、60° C、60°或120° D、30°

查看试题解析
4. 下列结论正确的是（）

A、各个面都是三角形的几何体是三棱锥 B、一平面截一棱锥得到一个棱锥和一个棱台 C、棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥 D、圆锥的顶点与底面圆周上的任意一点的连线都是母线

查看试题解析
5. 某四面体的三视图如图所示，该四面体的体积为（）

A、 $\frac{4}{3}$ B、2 C、 $\frac{8}{3}$ D、4

查看试题解析
6. 已知cos（ $α - \frac{π}{3}$ ）﹣cosα= $\frac{1}{3}$ ，则cos（ $α + \frac{π}{3}$ ）的值为（）

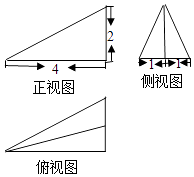A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、 $\frac{2}{3}$ D、﹣ $\frac{2}{3}$

查看试题解析
7. 设{a_n}是公比为正数的等比数列，a₁=2，a₃﹣4=a₂ ，则a₃=（）

A、2 B、﹣2 C、8 D、﹣8

查看试题解析
8. △ABC的内角A、B、C的对边分别为a、b、c．已知a= $\sqrt{5}$ ，c=2，cosA= $\frac{2}{3}$ ，则b=（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、3

查看试题解析
9. 已知不等式ax²+bx+2＞0的解集为{x|﹣1＜x＜2}，则不等式2x²+bx+a＜0的解集为（）

A、 ${x | - 1 < x < \frac{1}{2}}$ B、 ${x | x < - 1 ，或 x > \frac{1}{2}}$ C、{x|﹣2＜x＜1} D、{x|x＜﹣2，或x＞1}

查看试题解析
10. 已知各项均为正数的等差数列{a_n}的前20项和为100，那么a₃•a₁₈的最大值是（）

A、50 B、25 C、100 D、2 $\sqrt{20}$

查看试题解析
11. 对于任意实数x，不等式mx²+mx﹣1＜0恒成立，则实数m取值范围（）

A、（﹣∞，﹣4） B、（﹣∞，﹣4] C、（﹣4，0） D、（﹣4，0]

查看试题解析
12. 两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题．他们在沙滩上画点或用小石子表示数，按照点或小石子能排列的形状对数进行分类．如下图中实心点的个数5，9，14，20，…为梯形数．根据图形的构成，记此数列的第2013项为a₂₀₁₃ ，则a₂₀₁₃﹣5=（）

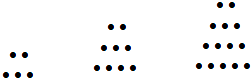A、2019×2013 B、2019×2012 C、1006×2013 D、2019×1006

查看试题解析

二、填空题

13. 不等式 $\frac{2}{x + 1}$ ＜1的解集是．

查看试题解析
14. 若函数f（x）=x+ $\frac{1}{x - 2}$ （x＞2）在x=a处取最小值，则a= ．

查看试题解析
15. 在等比数列中，已知a₃= $\frac{3}{2}$ ，s₃= $\frac{9}{2}$ ，求q= ．

查看试题解析
16. 已知tanα=2， $t a n (α - β) = - \frac{3}{5}$ ，则tanβ= ．

查看试题解析

三、解答题

17. 已知 $\vec{a}$ ， $\vec{b}$ 的夹角为120°，且| $\vec{a}$ |=4，| $\vec{b}$ |=2．求：

(1)、（ $\vec{a}$ ﹣2 $\vec{b}$ ）•（ $\vec{a}$ + $\vec{b}$ ）；

(2)、|3 $\vec{a}$ ﹣4 $\vec{b}$ |．

查看试题解析
18. 已知函数f（x）=4cosx•sin（x+ $\frac{π}{6}$ ）+a的最大值为2．

(1)、求a的值及f（x）的最小正周期；

(2)、求f（x）的单调递增区间．

查看试题解析
19. 在△ABC中，A、B、C的对边分别是a、b、c，且A、B、C成等差数列．△ABC的面积为 $\frac{\sqrt{3}}{2}$ ．

(1)、求：ac的值；

(2)、若b= $\sqrt{3}$ ，求：a，c 的值．

查看试题解析
20. 已知{a_n}是等差数列，{b_n}是等比数列，且b₂=3，b₃=9，a₁=b₁ ， a₁₄=b₄ ．
（Ⅰ）求{a_n}的通项公式；
（Ⅱ）设c_n=a_n+b_n ，求数列{c_n}的前n项和S_n ．

查看试题解析
21. 围建一个面积为360m²的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：m），修建此矩形场地围墙的总费用为y（单位：元）．
（Ⅰ）将y表示为x的函数：
（Ⅱ）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用．

查看试题解析
22. 已知点（1， $\frac{1}{6}$ ）是函数f（x）= $\frac{1}{2}$ a^x（a＞0，a≠1）图象上一点，等比数列{a_n}的前n项和为c﹣f（n）．数列{b_n}（b_n＞0）的首项为2c，前n项和满足 $\sqrt{S_{n}}$ = $\sqrt{S_{n - 1}}$ +1（n≥2）．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）若数列{ $\frac{1}{b_{n} b_{n + 1}}$ }的前n项和为T_n ，问使T_n＞ $\frac{1000}{2017}$ 的最小正整数n是多少？

查看试题解析