2016-2017学年湖北省宜昌市部分示范高中教学协作体高一下学期期末数学试卷

试卷更新日期：2017-08-07 类型：期末考试

进入出卷网下载

一、选择题

1. 已知a＞b＞0且c＜d，下列不等式中成立的一个是（）

A、a+c＞b+d B、a﹣c＞b﹣d C、ad＜bc D、 $\frac{a}{c}$ ＞ $\frac{b}{d}$

查看试题解析
2. 已知向量 $\vec{a}$ =（4，2），向量 $\vec{b}$ =（x，3），且 $\vec{a} ∥ \vec{b}$ ，那么x等于（）

A、8 B、7 C、6 D、5

查看试题解析
3. 在△ABC中，a=2 $\sqrt{3}$ ，b=2 $\sqrt{2}$ ，∠B=45°，则∠A=（）

A、30°或120° B、60° C、60°或120° D、30°

查看试题解析
4. 下列结论正确的是（）

A、各个面都是三角形的几何体是三棱锥 B、一平面截一棱锥得到一个棱锥和一个棱台 C、棱锥的侧棱长与底面多边形的边长相等，则该棱锥可能是正六棱锥 D、圆锥的顶点与底面圆周上的任意一点的连线都是母线

查看试题解析
5. 某四面体的三视图如图所示，该四面体的体积为（）

A、 $\frac{4}{3}$ B、2 C、 $\frac{8}{3}$ D、4

查看试题解析
6. 已知cos（ $α - \frac{π}{3}$ ）﹣cosα= $\frac{1}{3}$ ，则cos（ $α + \frac{π}{3}$ ）的值为（）

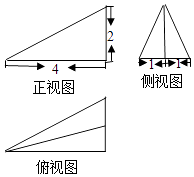A、 $\frac{1}{3}$ B、﹣ $\frac{1}{3}$ C、 $\frac{2}{3}$ D、﹣ $\frac{2}{3}$

查看试题解析
7. 设{a_n}是公比负数的等比数列，a₁=2，a₃﹣4=a₂ ，则a₃=（）

A、2 B、﹣2 C、8 D、﹣8

查看试题解析
8. △ABC的内角A、B、C的对边分别为a、b、c．已知a= $\sqrt{5}$ ，c=2，cosA= $\frac{2}{3}$ ，则b=（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、2 D、3

查看试题解析
9. 已知不等式ax²+bx+2＞0的解集为{x|﹣1＜x＜2}，则不等式2x²+bx+a＜0的解集为（）

A、 ${x | - 1 < x < \frac{1}{2}}$ B、 ${x | x < - 1 ，或 x > \frac{1}{2}}$ C、{x|﹣2＜x＜1} D、{x|x＜﹣2，或x＞1}

查看试题解析
10. 已知各项均为正数的等差数列{a_n}的前20项和为100，那么a₃•a₁₈的最大值是（）

A、50 B、25 C、100 D、2 $\sqrt{20}$

查看试题解析
11. 对于任意实数x，不等式mx²+mx﹣1＜0恒成立，则实数m取值范围（）

A、（﹣∞，﹣4） B、（﹣∞，﹣4] C、（﹣4，0） D、（﹣4，0]

查看试题解析
12. 两千多年前，古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题．他们在沙滩上画点或用小石子表示数，按照点或小石子能排列的形状对数进行分类．如下图中实心点的个数5，9，14，20，…为梯形数．根据图形的构成，记此数列的第2013项为a₂₀₁₃ ，则a₂₀₁₃﹣5=（）

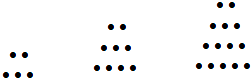A、2019×2013 B、2019×2012 C、1006×2013 D、2019×1006

查看试题解析

二、填空题

13. 不等式 $\frac{2}{x + 1}$ ＜1的解集是．

查看试题解析
14. 若函数f（x）=x+ $\frac{1}{x - 2}$ （x＞2）在x=a处取最小值，则a= ．

查看试题解析
15. 在等比数列中，已知a₃= $\frac{3}{2}$ ，s₃= $\frac{9}{2}$ ，求q= ．

查看试题解析
16. 已知tanα=2， $t a n (α - β) = - \frac{3}{5}$ ，则tanβ= ．

查看试题解析

三、解答题

17. 已知 $\vec{a}$ ， $\vec{b}$ 的夹角为120°，且| $\vec{a}$ |=4，| $\vec{b}$ |=2．求：

(1)、（ $\vec{a}$ ﹣2 $\vec{b}$ ）•（ $\vec{a}$ + $\vec{b}$ ）；

(2)、|3 $\vec{a}$ ﹣4 $\vec{b}$ |．

查看试题解析
18. 已知函数f（x）=4cosx•sin（x+ $\frac{π}{6}$ ）+a的最大值为2．

(1)、求a的值及f（x）的最小正周期；

(2)、求f（x）的单调递增区间．

查看试题解析
19. 在△ABC中，A、B、C的对边分别是a、b、c，且A、B、C成等差数列．△ABC的面积为 $\frac{\sqrt{3}}{2}$ ．

(1)、求：ac的值；

(2)、若b= $\sqrt{3}$ ，求：a，c 的值．

查看试题解析
20. 已知{a_n}是等差数列，{b_n}是等比数列，且b₂=3，b₃=9，a₁=b₁ ， a₁₄=b₄ ．
（Ⅰ）求{a_n}的通项公式；
（Ⅱ）设c_n=a_n+b_n ，求数列{c_n}的前n项和S_n ．

查看试题解析
21. 围建一个面积为360m²的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：m），修建此矩形场地围墙的总费用为y（单位：元）．
（Ⅰ）将y表示为x的函数：
（Ⅱ）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用．

查看试题解析
22. 已知点（1， $\frac{1}{6}$ ）是函数f（x）= $\frac{1}{2}$ a^x（a＞0，a≠1）图象上一点，等比数列{a_n}的前n项和为c﹣f（n）．数列{b_n}（b_n＞0）的首项为2c，前n项和满足 $\sqrt{S_{n}}$ = $\sqrt{S_{n - 1}}$ +1（n≥2）．
（Ⅰ）求数列{a_n}的通项公式；
（Ⅱ）若数列{ $\frac{1}{b_{n} b_{n + 1}}$ }的前n项和为T_n ，问使T_n＞ $\frac{1000}{2017}$ 的最小正整数n是多少？

查看试题解析