2017年内蒙古包头市青山区中考数学二模试卷
试卷更新日期:2017-08-07 类型:中考模拟
一、选择题
-
1. 计算2﹣(﹣1)2等于( )A、1 B、0 C、﹣1 D、32. 下列计算中,不正确的是( )A、﹣2x+3x=x B、6xy2÷2xy=3y C、(﹣2x2y)3=﹣6x6y3 D、2xy2•(﹣x)=﹣2x2y23. 函数y= 的自变量x的取值范围为( )A、x>2 B、x<2 C、x≤2 D、x≠24. 某校为了了解九年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在30~35次之间的频率是( )
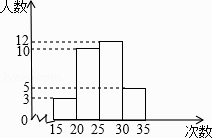 A、0.2 B、0.17 C、0.33 D、0.145. 下列方程中,没有实数根的是( )A、2x+3=0 B、x2﹣1=0 C、 = ﹣3 D、x2+x﹣1=06. 如图,过点C(﹣2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )
A、0.2 B、0.17 C、0.33 D、0.145. 下列方程中,没有实数根的是( )A、2x+3=0 B、x2﹣1=0 C、 = ﹣3 D、x2+x﹣1=06. 如图,过点C(﹣2,5)的直线AB分别交坐标轴于A(0,2),B两点,则tan∠OAB=( )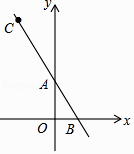 A、 B、 C、 D、7. 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )
A、 B、 C、 D、7. 如图是一个直三棱柱的立体图和主视图、俯视图,根据立体图上的尺寸标注,它的左视图的面积为( )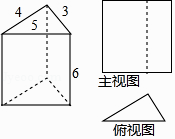 A、24 B、30 C、18 D、14.48. 时,代数式 的值是( )A、 B、 C、 D、9. 已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=( )A、4 B、 C、 D、10. 随机掷一枚质地均匀的硬币三次,则至少有一次反面朝上的概率是( )A、 B、 C、 D、11. 已知下列命题:
A、24 B、30 C、18 D、14.48. 时,代数式 的值是( )A、 B、 C、 D、9. 已知⊙O的半径是4,P是⊙O外的一点,且PO=8,从点P引⊙O的两条切线,切点分别是A,B,则AB=( )A、4 B、 C、 D、10. 随机掷一枚质地均匀的硬币三次,则至少有一次反面朝上的概率是( )A、 B、 C、 D、11. 已知下列命题:①16的平方根是±4
②若x=3,则x2﹣3x=0
③六边形的内角和是外角和的2倍
④顺次连接菱形四边中点的线段组成的四边形是矩形
其中原命题与逆命题均为真命题的个数是( )
A、1个 B、2个 C、3个 D、4个12. 如图,抛物线y=﹣ x2+ x+ 与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( ) A、(4,3) B、(5, ) C、(4, ) D、(5,3)
A、(4,3) B、(5, ) C、(4, ) D、(5,3)二、填空题
-
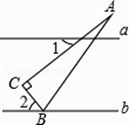
13. 分解因式:a2b+2ab2+b3= .14. 如图,已知直线a∥b,△ABC的顶点B在直线b上,∠C=90°,∠1=36°,则∠2的度数是 .
 15. 在综合实践课上,六名同学做的作品的数量(单位:件)分别是:5,7,3,x,6,4;若这组数据的平均数是5,则这组数据的中位数是件.16. 若关于x的方程x2+2mx+m2+3m﹣2=0有两个实数根x1、x2 , 则x1(x2+x1)+x22的最小值为 .17. 如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在 上的点D处,折痕交OA于点C,则 的长为 .
15. 在综合实践课上,六名同学做的作品的数量(单位:件)分别是:5,7,3,x,6,4;若这组数据的平均数是5,则这组数据的中位数是件.16. 若关于x的方程x2+2mx+m2+3m﹣2=0有两个实数根x1、x2 , 则x1(x2+x1)+x22的最小值为 .17. 如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在 上的点D处,折痕交OA于点C,则 的长为 . 18.
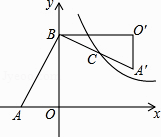
18.如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y= 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k= .
 19. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF= .
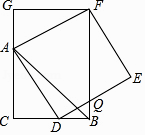
19. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF= . 20. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
20. 如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,
其中正确的结论的个数是 .
三、解答题
-
21. 在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
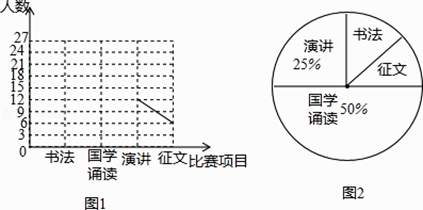 (1)、请求出九(2)全班人数;(2)、请把折线统计图补充完整;(3)、南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.22.
(1)、请求出九(2)全班人数;(2)、请把折线统计图补充完整;(3)、南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.22.甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
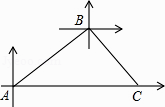 (1)、港口A与小岛C之间的距离;(2)、甲轮船后来的速度.23. 某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.(1)、若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?(2)、凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.(3)、若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)?24. 已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.
(1)、港口A与小岛C之间的距离;(2)、甲轮船后来的速度.23. 某批发市场有中招考试文具套装,其中A品牌的批发价是每套20元,B品牌的批发价是每套25元,小王需购买A、B两种品牌的文具套装共1000套.(1)、若小王按需购买A、B两种品牌文具套装共用22000元,则各购买多少套?(2)、凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000套文具套装,共用了y元,设A品牌文具套装买了x包,请求出y与x之间的函数关系式.(3)、若小王购买会员卡并用此卡按需购买1000套文具套装,共用了20000元,他计划在网店包邮销售这两种文具套装,每套文具套装小王需支付邮费8元,若A品牌每套销售价格比B品牌少5元,请你帮他计算,A品牌的文具套装每套定价不低于多少元时才不亏本(运算结果取整数)?24. 已知:如图,△ABC内接于⊙O,AB为直径,∠CBA的平分线交AC于点F,交⊙O于点D,DE⊥AB于点E,且交AC于点P,连结AD.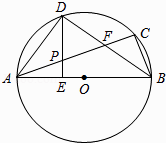 (1)、求证:∠DAC=∠DBA;(2)、求证:P是线段AF的中点;(3)、连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.25.
(1)、求证:∠DAC=∠DBA;(2)、求证:P是线段AF的中点;(3)、连接CD,若CD﹦3,BD﹦4,求⊙O的半径和DE的长.25.如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
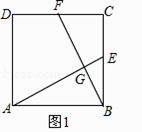 (1)、求证:AE⊥BF;(2)、
(1)、求证:AE⊥BF;(2)、将△BCF沿BF对折,得到△BPF(如图2),延长FP到BA的延长线于点Q,求sin∠BQP的值;
 (3)、
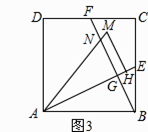
(3)、将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
 26. 如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
26. 如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.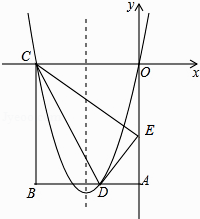 (1)、求OE的长及经过O,D,C三点抛物线的解析式;(2)、一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;(3)、若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
(1)、求OE的长及经过O,D,C三点抛物线的解析式;(2)、一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;(3)、若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.