2017年内蒙古包头市东河区中考数学一模试卷

试卷更新日期：2017-08-07 类型：中考模拟

进入出卷网下载

一、选择题

1. 在实数0，﹣π， $\sqrt{3}$ ，﹣4中，最小的数是（）

A、0 B、﹣π C、 $\sqrt{3}$ D、﹣4

查看试题解析
2. 某种计算机完成一次基本运算的时间约为0.000000005s，把0.000000005s用科学记数法可以表示为（）

A、0.5×10^﹣⁸s B、5×10^﹣⁹s C、5×10^﹣⁸s D、0.5×10^﹣⁹s

查看试题解析
3. 下列运算正确的是（）

A、（﹣2a³）²=﹣4a⁶ B、 $\sqrt{9}$ =±3 C、m²•m³=m⁶ D、x³+2x³=3x³

查看试题解析
4. 在Rt△ABC中，∠C=90°，sinA= $\frac{2}{3}$ ，那么tanB的值是（　　）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{\sqrt{5}}{3}$ C、 $\frac{2 \sqrt{5}}{5}$ D、 $\frac{2}{3}$

查看试题解析
5. 某班抽取6名学生参加体能测试，成绩如下：80，90，75，75，80，80，下列表述错误的是（）

A、平均数是80 B、极差是15 C、中位数是80 D、众数是75

查看试题解析
6. 不等式组 ${\begin{matrix} \frac{3 x - 5}{2} \leq x - 2 \\ 3 (x - 1) < 4 (x + 1) \end{matrix}$ 的解集是（）

A、x≤1 B、x＞﹣7 C、﹣7＜x≤1 D、无解

查看试题解析
7. 下列说法正确的是（）

A、为了了解我市今夏冰淇淋的质量，应采用普查的调查方式进行 B、鞋类销售商最感兴趣的是所销售的某种品牌鞋的尺码的平均数 C、明天我市会下雨是随机事件 D、某种彩票中奖的概率是1%，买100张该种彩票一定会中奖

查看试题解析
8. 已知圆锥的母线长是5cm，侧面积是15πcm² ，则这个圆锥底面圆的半径是（）

A、1.5cm B、3cm C、4cm D、6cm

查看试题解析
9. 如图，在△ABC中，∠C=90°，AC=BC，AB=2，点O为AB的中点，以点O为圆心作半圆与边AC相切于点D．则图中阴影部分的面积为（）

A、1﹣ $\frac{1}{4}$ π B、 $\frac{1}{2}$ ﹣ $\frac{π}{8}$ C、2﹣ $\frac{3 π}{4}$ D、2﹣ $\frac{1}{4}$ π

查看试题解析
10. 已知下列命题：
①各边相等的多边形是正多边形；
②相等的圆心角所对的弧相等；
③若a²=b² ，则a=b；
④若直线y=kx+b经过第一、二、四象限，则k＜0，b＞0．
其中原命题与逆命题都是真命题的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是（）

A、 $6 \sqrt{2}$ B、6 C、 $3 \sqrt{2}$ D、 $3 + 3 \sqrt{2}$

查看试题解析
12. 已知二次函数y=ax²+bx+c（a≠0）的图象如图所示，给下以下结论：
①2a﹣b=0；
②9a+3b+c＜0；
③关于x的一元二次方程ax²+bx+c+3=0有两个相等实数根；
④8a+c＜0．
其中正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 计算：﹣1⁴+ $\sqrt{12}$ +sin60°+（π﹣ $\sqrt{5}$ ）⁰= ．

查看试题解析
14. 化简： $1 - \frac{x + y}{x - 3 y} \div \frac{x^{2} - y^{2}}{x^{2} - 6 x y + 9 y^{2}}$ = ．

查看试题解析
15. 从长度分别为1、3、5、7的四条线段中任选三条作边，能构成三角形的概率为

查看试题解析
16. 若x₁ ， x₂是一元二次方程x²﹣2x﹣1=0的两个根，则x₁²﹣x₁+x₂的值为．

查看试题解析
17. 如图所示，Rt△ABC中，∠ACB=90°，点A坐标为（0，1），点B坐标为（0，﹣1），且∠ABC=30°，若反比例函数y= $\frac{k}{x}$ （k≠0）的图象经过点C，则k的值为．

查看试题解析
18. 如图，AB是⊙O的直径，弦CD⊥AB，垂足是G，F是CG的中点，延长AF交⊙O于E，CF=2，AF=3，则EF的长是．

查看试题解析
19. 如图，在四边形ABCD中，AD∥BC，∠C=90°，E为CD上一点，分别以EA，EB为折痕将两个角（∠D，∠C）向内折叠，点C，D恰好落在AB边的点F处．若AD=2，BC=3，则EF的长为．

查看试题解析
20. 如图，正方形ABCD的边长为1，以AB为直径作半圆，点P是CD中点，BP与半圆交于点Q，连结DQ，给出如下结论：①DQ=1；② $\frac{P Q}{B Q}$ = $\frac{3}{2}$ ；③S_△_PDQ= $\frac{1}{8}$ ；④cos∠ADQ= $\frac{3}{5}$ ，其中正确结论是（填写序号）

查看试题解析

三、解答题

21. 某校初三（1）班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题．

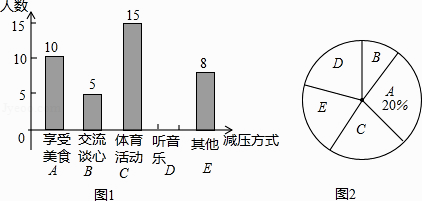(1)、初三（1）班接受调查的同学共有多少名；

(2)、补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数；

(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生；老师想从5名同学中任选两名同学进行交流，直接写出选取的两名同学都是女生的概率．

查看试题解析
22.
如图，在大楼AB的正前方有一斜坡CD，CD=4米，坡角∠DCE=30°，小红在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的点D处测得楼顶B的仰角为45°，其中点A、C、E在同一直线上．

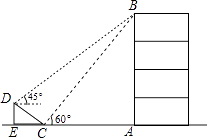(1)、求斜坡CD的高度DE；

(2)、求大楼AB的高度（结果保留根号）

查看试题解析
23. 某文具店购进A，B两种钢笔，若购进A种钢笔2支，B种钢笔3支，共需90元；购进A种钢笔3支，B种钢笔5支，共需145元．

(1)、求A、B两种钢笔每支各多少元？

(2)、若该文具店要购进A，B两种钢笔共90支，总费用不超过1588元，并且A种钢笔的数量少于B种钢笔的数量，那么该文具店有哪几种购买方案？

(3)、文具店以每支30元的价格销售B种钢笔，很快销售一空，于是，文具店决定在进价不变的基础上再购进一批B种钢笔，涨价卖出，经统计，B种钢笔售价为30元时，每月可卖68支；每涨价1元，每月将少卖4支，设文具店将新购进的B种钢笔每支涨价a元（a为正整数），销售这批钢笔每月获利W元，试求W与a之间的函数关系式，并且求出B种铅笔销售单价定为多少元时，每月获利最大？最大利润是多少元？

查看试题解析
24. 如图，AB是O的直径，AE交O于点E，且与O的切线CD互相垂直，垂足为D．

(1)、求证：∠EAC=∠CAB；

(2)、若CD=4，AD=8：①求O的半径；②求tan∠BAE的值．

查看试题解析
25. 解答题

(1)、如图1，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．求证：CE=CF；

(2)、如图2，在正方形ABCD中，E是AB上一点，G是AD上一点，如果∠GCE=45°，请你利用（1）的结论证明：GE=BE+GD．

(3)、运用（1）（2）解答中所积累的经验和知识，完成下题：
如图3，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，E是AB上一点，且∠DCE=45°，BE=4，DE=10，求直角梯形ABCD的面积．

查看试题解析
26.
如图，已知直线y=﹣x+3与x轴、y轴分别交于A，B两点，抛物线y=﹣x²+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以 $\sqrt{2}$ 个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．

(1)、求抛物线的解析式；

(2)、当t为何值时，△APQ为直角三角形；

(3)、过点P作PE∥y轴，交AB于点E，过点Q作QF∥y轴，交抛物线于点F，连接EF，当EF∥PQ时，求点F的坐标．

查看试题解析