2017年江苏省镇江市润州区中考数学二模试卷
试卷更新日期:2017-08-07 类型:中考模拟
一、填空题
-
1. ﹣ 的倒数是2. 计算: = .3. 分解因式:2x2﹣12x+18= .4. 函数y= 中,自变量x的取值范围是 .5. 若一个多边形的内角和等于720°,则这个多边形是边形.6. 若关于x的一元二次方程kx2+2x﹣1=0有两个实数根,则k的取值范围是 .7. △ABC中,D、E分别在AB、AC上,DE∥BC,AD=1,BD=3,则△ADE与△ABC的面积之比为 .
 8. 如图,四边形ABCD是⊙O的内接四边形,∠B=148°24′,则∠AOC的角度为 .
8. 如图,四边形ABCD是⊙O的内接四边形,∠B=148°24′,则∠AOC的角度为 . 9. 如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB= .
9. 如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB= . 10. 圆锥底面圆的半径为3,高长为4,它的表面积等于(结果保留π).11. 如图,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为 .
10. 圆锥底面圆的半径为3,高长为4,它的表面积等于(结果保留π).11. 如图,已知点C(1,0),直线y=﹣x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为 .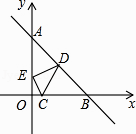 12. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是 .
12. 抛物线y=ax2+bx+3(a≠0)过A(4,4),B (2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是 .二、选择题
-
13.
如图是一些完全相同的小正方体搭成的几何体的三视图.这个几何体只能是( )
 A、
A、 B、
B、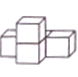 C、
C、 D、
D、 14. 如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )
14. 如图,数轴上的四个点A、B、C、D位置如图所示,它们分别对应四个实数a、b、c、d,若a+c=0,AB<BC,则下列各式正确的是( )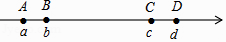 A、bc>0 B、b﹣d>0 C、b+c>0 D、|a|>|d|15. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣ ,3),反比例函数y= 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A、bc>0 B、b﹣d>0 C、b+c>0 D、|a|>|d|15. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,顶点C的坐标为(﹣ ,3),反比例函数y= 的图象与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( ) A、4 B、﹣4 C、2 D、﹣216. 已知二次函数y=ax2+bx+c,函数y与自变量x的部分对应值如下表:
A、4 B、﹣4 C、2 D、﹣216. 已知二次函数y=ax2+bx+c,函数y与自变量x的部分对应值如下表:x
…
﹣4
﹣3
﹣2
﹣1
0
…
y
…
3
﹣2
﹣5
﹣6
﹣5
…
则下列判断中正确的是( )
A、抛物线开口向下 B、抛物线与y轴交于正半轴 C、方程ax2+bx+c=0的正根在1与2之间 D、当x=﹣3时的函数值比x=1.5时的函数值大17. 如图,正六边形A1B1C1D1E1F1的边长为2,正六边形A2B2C2D2E2F2的外接圆与正六边形A1B1C1D1E1F1的各边相切,正六边形A3B3C3D3E3F3的外接圆与正六边形A2B2C2D2E2F2的各边相切,…按这样的规律进行下去,A10B10C10D10E10F10的边长为( ) A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
18. 化简求值(1)、计算: ﹣3tan230°+2(2)、化简: ÷(1+ )19. 解方程(1)、解方程: + =4(2)、解不等式组 ,并把它们的解集在数轴上表示出来.20. 王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
 (1)、根据图中提供的数据列出如下统计表:
(1)、根据图中提供的数据列出如下统计表:平均成绩(分)
中位数(分)
众数(分)
方差(S2)
王华
80
b
80
d
张伟
a
85
c
260
则a= , b= , c= , d= ,
(2)、将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .(3)、现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?21. 如图,在△ABC和△BCD中,AB=DC,AC=DB,AC、DB交于点M. (1)、求证:△ABC≌△DCB;(2)、作CN∥BD,BN∥AC,CN交BN于点N,求证:四边形BNCM是菱形.22. 小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).(1)、如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .(2)、如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.(3)、从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)23. 如图,已知△ABC的三个顶点的坐标分别为A(﹣2,2)、B(﹣5,0)、C(﹣1,0),P(a,b)是△ABC的边AC上一点:
(1)、求证:△ABC≌△DCB;(2)、作CN∥BD,BN∥AC,CN交BN于点N,求证:四边形BNCM是菱形.22. 小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).(1)、如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .(2)、如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.(3)、从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)23. 如图,已知△ABC的三个顶点的坐标分别为A(﹣2,2)、B(﹣5,0)、C(﹣1,0),P(a,b)是△ABC的边AC上一点: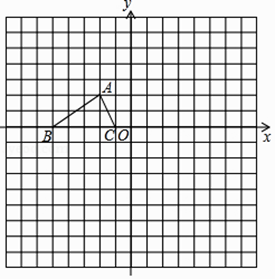 (1)、将△ABC绕原点O逆时针旋转90°得到△A1B1C1 , 请在网格中画出△A1B1C1 , 旋转过程中点A所走的路径长为 .(2)、将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2 , 并写出点A2的坐标:A2().(3)、若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为(直接写出结果).24. 如图,一次函数y1=k1x+b与反比例函数y2= 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)、将△ABC绕原点O逆时针旋转90°得到△A1B1C1 , 请在网格中画出△A1B1C1 , 旋转过程中点A所走的路径长为 .(2)、将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2 , 并写出点A2的坐标:A2().(3)、若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为(直接写出结果).24. 如图,一次函数y1=k1x+b与反比例函数y2= 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C. (1)、m= , k1=;(2)、当x的取值是时,k1x+b> ;(3)、过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.25. 如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度.(参考数据: ≈1.4, ≈1.7,结果保留整数)
(1)、m= , k1=;(2)、当x的取值是时,k1x+b> ;(3)、过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.25. 如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度.(参考数据: ≈1.4, ≈1.7,结果保留整数) 26. 如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB.
26. 如图,AB是⊙O直径,OD⊥弦BC于点F,且交⊙O于点E,且∠AEC=∠ODB. (1)、判断直线BD和⊙O的位置关系,并给出证明;(2)、当tan∠AEC= ,BC=8时,求OD的长.27. 已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点.
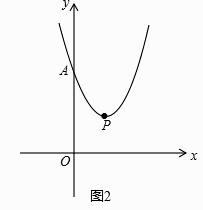
(1)、判断直线BD和⊙O的位置关系,并给出证明;(2)、当tan∠AEC= ,BC=8时,求OD的长.27. 已知直线m∥n,点C是直线m上一点,点D是直线n上一点,CD与直线m、n不垂直,点P为线段CD的中点. (1)、操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .(2)、猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)、延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.28. 已知抛物线y=x2+bx+c的顶点为P,与y轴交于点A,与直线OP交于点B.(1)、如图1,若点P的横坐标为1,点B的坐标为(3,6),试确定抛物线的解析式;
(1)、操作发现:直线l⊥m,l⊥n,垂足分别为A、B,当点A与点C重合时(如图①所示),连接PB,请直接写出线段PA与PB的数量关系: .(2)、猜想证明:在图①的情况下,把直线l向上平移到如图②的位置,试问(1)中的PA与PB的关系式是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)、延伸探究:在图②的情况下,把直线l绕点A旋转,使得∠APB=90°(如图③所示),若两平行线m、n之间的距离为2k.求证:PA•PB=k•AB.28. 已知抛物线y=x2+bx+c的顶点为P,与y轴交于点A,与直线OP交于点B.(1)、如图1,若点P的横坐标为1,点B的坐标为(3,6),试确定抛物线的解析式;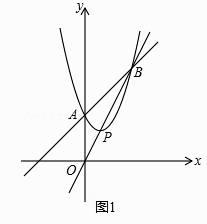 (2)、在(1)的条件下,若点M是直线AB下方抛物线上的一点,且S△ABM=3,求点M的坐标;(3)、如图2,若点P在第一象限,且PA=PO,过点P作PD⊥x轴于点D.将抛物线y=x2+bx+c平移,平移后的抛物线经过点A、D,该抛物线与x轴的另一个交点为C,请探究四边形OABC的形状,并说明理由.
(2)、在(1)的条件下,若点M是直线AB下方抛物线上的一点,且S△ABM=3,求点M的坐标;(3)、如图2,若点P在第一象限,且PA=PO,过点P作PD⊥x轴于点D.将抛物线y=x2+bx+c平移,平移后的抛物线经过点A、D,该抛物线与x轴的另一个交点为C,请探究四边形OABC的形状,并说明理由.