2017年江苏省盐城市响水县中考数学二模试卷

试卷更新日期：2017-08-07 类型：中考模拟

进入出卷网下载

一、选择题

1. 数﹣1， $\sqrt{5}$ ，0，2中最大的数是（）

A、﹣1 B、 $\sqrt{5}$ C、0 D、2

查看试题解析
2. 若a＜b，则下列各式中一定正确的是（）

A、ab＜0 B、ab＞0 C、a﹣b＞0 D、﹣a＞﹣b

查看试题解析
3. 如图，AB是⊙O直径，点C为⊙O上一点，∠C=20°，则∠BOC度数为（）

A、20° B、30° C、40° D、60°

查看试题解析
4. 如图是某几何题的三视图，下列判断正确的是（）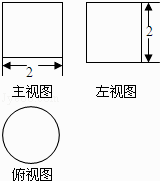

A、几何体是圆柱体，高为2 B、几何体是圆锥体，高为2 C、几何体是圆柱体，半径为2 D、几何体是圆锥体，半径为2

查看试题解析
5. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）

A、560（1+x）²=315 B、560（1﹣x）²=315 C、560（1﹣2x）²=315 D、560（1﹣x²）=315

查看试题解析
6.
如图，在△ABC中，∠C=90°，M是AB的中点，动点P从点A出发，沿AC方向匀速运动到终点C，动点Q从点C出发，沿CB方向匀速运动到终点B．已知P，Q两点同时出发，并同时到达终点，连接MP，MQ，PQ．在整个运动过程中，△MPQ的面积大小变化情况是（）

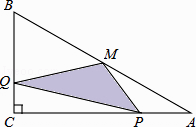A、一直增大 B、一直减小 C、先减小后增大 D、先增大后减少

查看试题解析

二、填空题

7. |﹣ $\frac{1}{3}$ |= ．

查看试题解析
8. 请写一个图象在第二、四象限的反比例函数解析式：．

查看试题解析
9. 一组数据8，7，8，6，6，8的众数是．

查看试题解析
10. 分解因式：3x²﹣3y²= ．

查看试题解析
11. 一元二次方程x²=x的解为．

查看试题解析
12. 已知一元二次方程x²﹣4x+3=0的两根x₁、x₂ ，则x₁²﹣4x₁+x₁x₂= ．

查看试题解析
13. 一个圆锥的母线长为4，侧面积为8π，则这个圆锥的底面圆的半径是．

查看试题解析
14. 如图，AB是⊙O的直径，点E为BC的中点，AB=4，∠BED=120°，则图中阴影部分的面积之和是．

查看试题解析
15. 已知：如图，在平面直角坐标系中，抛物线y=ax²+x的对称轴为直线x=2，顶点为A．点P为抛物线对称轴上一点，连结OA、OP．当OA⊥OP时，P点坐标为．

查看试题解析
16. 如图，在四边形ABCD中，AB⊥BC，AD∥BC，∠BCD=120°，BC=2，AD=DC．P为四边形ABCD边上的任意一点，当∠BPC=30°时，CP的长为．

查看试题解析

三、解答题

17. 计算：2^﹣¹+4cos45°﹣（π﹣2013）⁰﹣ $\sqrt{8}$ ．

查看试题解析
18. 解不等式组 ${\begin{matrix} 1 - 2 (x - 1) \leq 5 \\ \frac{3 x - 2}{2} < x + \frac{1}{2} \end{matrix}$ ．

查看试题解析
19. 化简再求值： $\frac{m}{m^{2} - n^{2}}$ ÷（1﹣ $\frac{n}{m + n}$ ），其中m= $\sqrt{3}$ +1，n=1﹣ $\sqrt{2}$ ．

查看试题解析
20. 某校初三（1）班的同学踊跃为“希望工程”捐款，根据捐款情况（捐款数为正数）制作以下统计图表，但班长不小心把墨水滴在统计表上，部分数据看不清楚．根据图表中现有信息解决下列问题：
捐款
人数
0～20元
21～40元
41～60元
61～80元
6
81元以上
4

(1)、全班有多少人捐款？

(2)、如果捐款0～20元的人数在扇形统计图中所占的圆心角为72°，那么捐款21～40元的有多少人？

查看试题解析
21. 在甲、乙两个不透明的布袋里，都装有3个大小、材质完全相同的小球，其中甲袋中的小球上分别标有数字0，1，2；乙袋中的小球上分别标有数字﹣1，﹣2，0．现从甲袋中任意摸出一个小球，记其标有的数字为x，再从乙袋中任意摸出一个小球，记其标有的数字为y，以此确定点M的坐标（x，y）．

(1)、请你用画树状图或列表的方法，写出点M所有可能的坐标；

(2)、求点M（x，y）在函数y=﹣ $\frac{2}{x}$ 的图象上的概率．

查看试题解析
22.
甲、乙两条轮船同时从港口A出发，甲轮船以每小时30海里的速度沿着北偏东60°的方向航行，乙轮船以每小时15海里的速度沿着正东方向行进，1小时后，甲船接到命令要与乙船会合，于是甲船改变了行进的速度，沿着东南方向航行，结果在小岛C处与乙船相遇．假设乙船的速度和航向保持不变，求：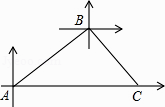

(1)、港口A与小岛C之间的距离；

(2)、甲轮船后来的速度．

查看试题解析
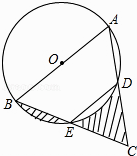
23. 已知四边形ABCD是边长为2的菱形，∠BAD=60°，对角线AC与BD交于点O，过点O的直线EF交AD于点E，交BC于点F．

(1)、求证：△AOE≌△COF；

(2)、若∠EOD=30°，求CE的长．

查看试题解析
24. 如图，PA、PB分别与⊙O相切于点A、B，点M在PB上，且OM∥AP，MN⊥AP，垂足为N．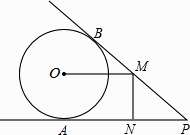

(1)、求证：OM=AN；

(2)、若⊙O的半径R=3，PA=9，求OM的长．

查看试题解析
25. 某车间的甲、乙两名工人分别同时生产500只同一型号的零件，他们生产的零件y（只）与生产时间x（分）的函数关系的图象如图所示．根据图象提供的信息解答下列问题：

(1)、甲每分钟生产零件只；乙在提高生产速度之前已生产了零件
只；

(2)、若乙提高速度后，乙的生产速度是甲的2倍，请分别求出甲、乙两人生产全过程中，生产的零件y（只）与生产时间x（分）的函数关系式；

(3)、当两人生产零件的只数相等时，求生产的时间；并求出此时甲工人还有多少只零件没有生产．

查看试题解析
26.
如图，在平面直角坐标系中，二次函数y=x²+bx+c的对称轴为经过点（1，0）的直线，其图象与x轴交于点A、B，且过点C（0，﹣3），其顶点为D．

(1)、求这个二次函数的解析式及顶点坐标；

(2)、在y轴上找一点P（点P与点C不重合），使得∠APD=90°，求点P的坐标；

(3)、在（2）的条件下，将△APD沿直线AD翻折得到△AQD，求点Q的坐标．

查看试题解析
27.
一透明的敞口正方体容器ABCD﹣A′B′C′D′装有一些液体，棱AB始终在水平桌面上，容器底部的倾斜角为α（∠CBE=α，如图1所示）．探究如图1，液面刚好过棱CD，并与棱BB′交于点Q，此时液体的形状为直三棱柱，其三视图及尺寸如图2所示．

解决问题：

(1)、CQ与BE的位置关系是， BQ的长是dm；

(2)、求液体的体积；（参考算法：直棱柱体积V_液=底面积S_△_BCQ×高AB）

(3)、求α的度数．（注：sin49°=cos41°= $\frac{3}{4}$ ，tan37°= $\frac{3}{4}$ ）

(4)、延伸：在图4的基础上，于容器底部正中间位置，嵌入一平行于侧面的长方形隔板（厚度忽略不计），得到图5，隔板高NM=1dm，BM=CM，NM⊥BC．继续向右缓慢旋转，当α=60°时，通过计算，判断溢出容器的液体能否达到4dm³ ．

查看试题解析

捐款	人数
0～20元
21～40元
41～60元
61～80元	6
81元以上	4