2017年江苏省南京市玄武区中考数学二模试卷
试卷更新日期:2017-08-07 类型:中考模拟
一、选择题
-
1. 2的相反数是( )A、2 B、 C、﹣2 D、﹣2. 氢原子的半径大约是0.000 0077m,将数据0.000 0077用科学记数法表示为( )A、0.77×10﹣5 B、0.77×10﹣6 C、7.7×10﹣5 D、7.7×10﹣63. ﹣ 介于( )A、﹣4与﹣3之间 B、﹣3与﹣2之间 C、﹣2与﹣1之间 D、﹣1与0之间4. 下列平面图形,既是中心对称图形,又是轴对称图形的是( )A、等腰三角形 B、正五边形 C、平行四边形 D、矩形5. 如图是一个几何体的三视图,这个几何体是( )
 A、四棱柱 B、三棱柱 C、三棱锥 D、圆锥6. 如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )
A、四棱柱 B、三棱柱 C、三棱锥 D、圆锥6. 如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )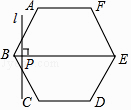 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
7. 8的算术平方根是;8的立方根是 .8. 要使式子 在实数范围内有意义,则x的取值范围是 .9. 计算 = .10. 已知反比例函数y= 的图象经过点A(﹣2,3),则当x=﹣1时,y= .11. 某班的中考英语口语考试成绩如表:
考试成绩/分
30
29
28
27
26
学生数/人
3
15
13
6
3
则该班中考英语口语考试成绩的众数比中位数多分.
12. 若方程x2﹣12x+5=0的两根分别为a,b,则a2b+ab2的值为 .13. 若圆锥的高是8cm,母线长是10cm,则这个圆锥的侧面积是cm2(结果保留π).14. 若一个正多边形的每一个外角都是30°,则这个正多边形的边数为 .15. 如图,在⊙O的内接六边形ABCDEF中,∠A+∠C=220°,则∠E=°. 16. 如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 .
16. 如图,在△ABC中,∠A=45°,∠B=60°,AB=4,P是BC边上的动点(不与B,C重合),点P关于直线AB,AC的对称点分别为M,N,则线段MN长的取值范围是 .
三、解答题
-
17. 解答题(1)、解不等式组 并把它的解集在数轴上表示出来.
 (2)、解方程 =1﹣ .18. 先化简代数式1﹣ ÷ ,并从﹣1,0,1,3中选取一个合适的数代入求值.19. 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
(2)、解方程 =1﹣ .18. 先化简代数式1﹣ ÷ ,并从﹣1,0,1,3中选取一个合适的数代入求值.19. 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.上网查找学习资源方式频数分布表
查找方式
频数
频率
搜索引擎
16
32%
专题网站
15
a
在线网校
4
8%
试题题库
10
20%
其他
b
10%
(1)、频数分布表中a,b的值:a=;b=;(2)、补全频数分布直方图;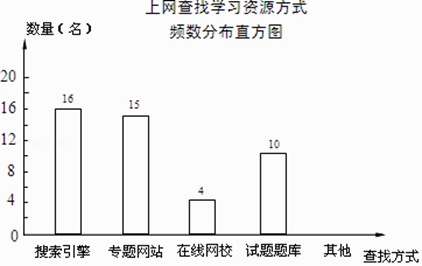 (3)、若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?20. 从2名男生和3名女生中随机抽取运动会志愿者.求下列事件的概率:(1)、抽取1名,恰好是女生的概率为;(2)、抽取2名,恰好是1名男生和1名女生.21. 如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF.
(3)、若全校有1000名学生,估计该校利用搜索引擎上网查找学习资源的学生有多少名?20. 从2名男生和3名女生中随机抽取运动会志愿者.求下列事件的概率:(1)、抽取1名,恰好是女生的概率为;(2)、抽取2名,恰好是1名男生和1名女生.21. 如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF. (1)、求证:△AFD≌△CEB;(2)、若∠CBE=∠BAC,四边形ABCD是怎样的四边形?证明你的结论.22. 某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?23. 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.
(1)、求证:△AFD≌△CEB;(2)、若∠CBE=∠BAC,四边形ABCD是怎样的四边形?证明你的结论.22. 某商场销售一批衬衫,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,商场采取了降价措施.假设在一定范围内,衬衫的单价每降1元,商场平均每天可多售出2件.如果降价后商场销售这批衬衫每天盈利1250元,那么衬衫的单价降了多少元?23. 如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为60°和35°,已知大桥BC的长度为100m,且与地面在同一水平面上.求热气球离地面的高度.(结果保留整数,参考数据:sin35°≈ ,cos35°≈ ,tan35°≈ , ≈1.7)
 24. 已知二次函数y=x2﹣(a﹣1)x+a﹣2,其中a是常数.
24. 已知二次函数y=x2﹣(a﹣1)x+a﹣2,其中a是常数. (1)、求证:不论a为何值,该二次函数的图象与x轴一定有公共点;(2)、当a=4时,该二次函数的图象顶点为A,与x轴交于B,D两点,与y轴交于C点,求四边形ABCD的面积.25. 如图①,在一条笔直的公路上有M、P、N三个地点,M、P两地相距20km,甲开汽车,乙骑自行车分别从M、P两地同时出发,匀速前往N地,到达N地后停止运动.已知乙骑自行车的速度为20km/h,甲,乙两人之间的距离y(km)与乙行驶的时间t(h)之间的关系如图②所示.
(1)、求证:不论a为何值,该二次函数的图象与x轴一定有公共点;(2)、当a=4时,该二次函数的图象顶点为A,与x轴交于B,D两点,与y轴交于C点,求四边形ABCD的面积.25. 如图①,在一条笔直的公路上有M、P、N三个地点,M、P两地相距20km,甲开汽车,乙骑自行车分别从M、P两地同时出发,匀速前往N地,到达N地后停止运动.已知乙骑自行车的速度为20km/h,甲,乙两人之间的距离y(km)与乙行驶的时间t(h)之间的关系如图②所示. (1)、M、N两地之间的距离为km;(2)、求线段BC所表示的y与t之间的函数表达式;(3)、若乙到达N地后,甲,乙立即以各自原速度返回M地,请在图②所给的直角坐标系中补全函数图象.26. 如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.
(1)、M、N两地之间的距离为km;(2)、求线段BC所表示的y与t之间的函数表达式;(3)、若乙到达N地后,甲,乙立即以各自原速度返回M地,请在图②所给的直角坐标系中补全函数图象.26. 如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB. (1)、求证:PB是⊙O的切线;(2)、若PC=9,AB=6 ,
(1)、求证:PB是⊙O的切线;(2)、若PC=9,AB=6 ,①求图中阴影部分的面积;
27. 解答题(1)、问题背景如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为BmC上一动点(不与B,C重合),求证: PA=PB+PC.
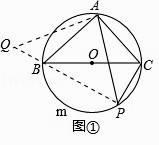
小明同学观察到图中自点A出发有三条线段AB,AP,AC,且AB=AC,这就为旋转作了铺垫.于是,小明同学有如下思考过程:
第一步:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);
第二步:证明Q,B,P三点共线,进而原题得证.
请你根据小明同学的思考过程完成证明过程.
(2)、类比迁移如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.
 (3)、拓展延伸
(3)、拓展延伸如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB= AC,AB⊥AC,垂足为A,则OC的最小值为 .
