2017年江苏省淮安市中考数学模拟试卷

试卷更新日期：2017-08-07 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣6的相反数是（）

A、﹣6 B、﹣ $\frac{1}{6}$ C、 $\frac{1}{6}$ D、6

查看试题解析
2. 函数y= $\sqrt{x + 1}$ 中自变量x的取值范围是（）

A、x＞﹣1 B、x≥﹣1 C、x＜﹣1 D、x≤﹣1

查看试题解析
3. 下列运算正确的是（）

A、2a+3b=5ab B、a²•a³=a⁵ C、（2a）³=6a ³ D、a⁶+a³=a⁹

查看试题解析
4. 用5个完全相同的小正方体组合成如图所示的立体图形，它的主视图为（）

A、 B、 C、 D、

查看试题解析
5. 一个盒子里有完全相同的三个小球，球上分别标有数字﹣2，1，4．随机摸出一个小球（不放回），其数字为p，再随机摸出另一个小球其数字记为q，则满足关于x的方程x²+px+q=0有实数根的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 体育课上，某班两名同学分别进行了5次短跑训练，要判断哪一名同学的成绩比较稳定，通常需要比较这两名学生成绩的（）

A、平均数 B、频数分布 C、中位数 D、方差

查看试题解析
7. 如图，在平面直角坐标系中，点A、B均在函数 $y = \frac{k}{x}$ （k＞0，x＞0）的图象上，⊙A与x轴相切，⊙B与y轴相切．若点B的坐标为（1，6），⊙A的半径是⊙B的半径的2倍，则点A的坐标为（）

A、（2，2） B、（2，3） C、（3， 2） D、（4， $\frac{3}{2}$ ）

查看试题解析

二、填空题

8. 据有关资料显示，长江三峡工程电站的总装机容量是18200000千瓦，请你用科学记数法表示电站的总装机容量，应记为千瓦．

查看试题解析
9. 因式分解：9x²﹣y²﹣4y﹣4= ．

查看试题解析
10. 关于x的方程x²﹣（2m﹣1）x+m²﹣1=0的两实数根为x₁ ， x₂ ，且x₁²+x₂²=3，则m= ．

查看试题解析
11. 一个圆锥的高为4cm，底面圆的半径为3cm，则这个圆锥的侧面积为．

查看试题解析
12. 如图，⊙C过原点，且与两坐标轴分别交于点A，点B，点A的坐标为（0，3），M是第三象限内弧OB上一点，∠BMO=120°，则⊙C的半径为．

查看试题解析
13. 已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表：
x
…
﹣1
0
1
2
3
…
y
…
10
5
2
1
2
…
则当y＜5时，x的取值范围是．

查看试题解析
14. 如图，三个小正方形的边长都为1，则图中阴影部分面积的和是（结果保留π）．

查看试题解析
15.
如图，△ABC是等腰直角三角形，AC=BC=a，以斜边AB上的点O为圆心的圆分别与AC，BC相切于点E，F，与AB分别交于点G，H，且EH的延长线和CB的延长线交于点D，则CD的长为．

查看试题解析
16. 如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=5，AC=2，则DF的长为．

查看试题解析

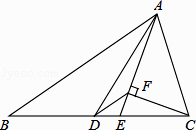
三、解答题

17. 计算题

(1)、2017⁰﹣|﹣sin45°|cos45°+ $\sqrt{{(- 3)}^{2}}$ ﹣（﹣ $\frac{1}{4}$ ）^﹣¹

(2)、 ${\begin{matrix} \frac{2 (x + y)}{3} - \frac{x + y}{4} = - \frac{1}{12} \\ 3 (x + y) - 2 (x - y) = 3 \end{matrix}$ ．

查看试题解析
18. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{2 x}$ ÷ $\frac{x^{2} - 2 x}{x^{2}}$ +1，在0，1，2三个数中选一个合适的，代入求值．

查看试题解析
19. 如图，在正方形ABCD内有一点P满足AP=AB，PB=PC，连接AC、PD．
求证：

(1)、△APB≌△DPC；

(2)、∠BAP=2∠PAC．

查看试题解析
20. 甲、乙两校分别有一男一女共4名教师报名到农村中学支教．

(1)、若从甲、乙两校报名的教师中分别随机选1名，则所选的2名教师性别相同的概率是．

(2)、若从报名的4名教师中随机选2名，用列表或画树状图的方法求出这2名教师来自同一所学校的概率．

查看试题解析
21. 为了解“数学思想作为对学习数学帮助有多大？”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查，并将调查得到的数据用下面的扇形图和下表来表示（图、表都没制作完成）．
选项
帮助很大
帮助较大
帮助不大
几乎没有帮助
人数
a
543
269
b
根据图、表提供的信息．

(1)、请问：这次共有多少名学生参与了问卷调查？

(2)、算出表中a、b的值．
（注：计算中涉及到的“人数”均精确到1）

查看试题解析
22.
如图，在南北方向的海岸线MN上，有A、B两艘巡逻船，现均收到故障船C的求救信号．已知A、B两船相距100（ $\sqrt{3}$ +1）海里，船C在船A的北偏东60°方向上，船C在船B的东南方向上，MN上有一观测点D，测得船C正好在观测点D的南偏东75°方向上．

(1)、分别求出A与C，A与D间的距离AC和AD（如果运算结果有根号，请保留根号）．

(2)、已知距离观测点D处100海里范围内有暗礁，若巡逻船A沿直线AC去营救船C，在去营救的途中有无触礁的危险？（参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

查看试题解析
23. 如图，AD是⊙O的切线，切点为A，AB是⊙O的弦．过点B作BC∥AD，交⊙O于点C，连接AC，过点C作CD∥AB，交AD于点D．连接AO并延长交BC于点M，交过点C的直线于点P，且∠BCP=∠ACD．

(1)、判断直线PC与⊙O的位置关系，并说明理由；

(2)、若AB=9，BC=6．求PC的长．

查看试题解析
24. 水果店王阿姨到水果批发市场打算购进一种水果销售，经过还价，实际价格每千克比原来少2元，发现原来买这种水果80千克的钱，现在可买88千克．

(1)、现在实际购进这种水果每千克多少元？

(2)、王阿姨准备购进这种水果销售，若这种水果的销售量y（千克）与销售单价x（元/千克）满足如图所示的一次函数关系．
①求y与x之间的函数关系式；
②请你帮王阿姨拿个主意，将这种水果的销售单价定为多少时，能获得最大利润？最大利润是多少？（利润=销售收入﹣进货金额）

查看试题解析
25.
如图，在平面直角坐标系中，已知点A（0，1），直线l：y=﹣1．动点P满足条件：
①P在这个平面直角坐标系中；
②P到A的距离和P到l的距离相等；

(1)、求点P所经过的轨迹方程，并在网格中绘制这个图象．（提示：平面直角坐标系中两点之间的距离可以通过勾股定理来求得）

(2)、已知直线y=kx+1，小明同学说，这条直线与（1）中所绘的图象有两个交点？你能说明小明为什么这么说吗？

(3)、经过了上述的计算、绘图，小明发现，如果第（2）问的两个交点分别为B、C，那么，过BC的中点M作直线l的垂线，垂足为H，连接BH、CH，所得到的三角形BCH是个特殊的三角形，你能说明它是什么三角形吗？为什么？

查看试题解析
26.
如图①，正方形ABCD中，点A，B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A→B→C→D→A匀速运动，同时动点Q以相同的速度在x轴正半轴上运动，当点P到达A点时，两点同时停止运动，设运动的时间为t秒．

(1)、
当P点在边AB上运动时点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；

(2)、求正方形边长及顶点C的坐标；

(3)、在（1）中，设△OPQ的面积为S，求S与t的函数关系式并写出自变量的取值范围．

(4)、如果点P、Q保持原速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相等？若能，写出所有符合条件的t的值；若不能，请说明理由．

查看试题解析

选项	帮助很大	帮助较大	帮助不大	几乎没有帮助
人数	a	543	269	b

x	…	﹣1	0	1	2	3	…
y	…	10	5	2	1	2	…